Центральная
предельная теорема (общий случай)
Как уже отмечалось, нормальные
распределения в настоящее время часто используют в вероятностных моделях в
различных прикладных областях. В чем причина такой широкой распространенности
этого двухпараметрического семейства распределений? Она проясняется следующей
теоремой.
Центральная
предельная теорема (для разнораспределенных слагаемых). Пусть X1, X2,…, Xn,… - независимые случайные величины с
математическими ожиданиями М(X1), М(X2),…, М(Xn), … и дисперсиями D(X1), D(X2),…, D(Xn), … соответственно. Пусть
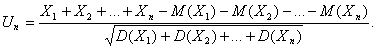
Тогда при справедливости некоторых
условий, обеспечивающих малость вклада любого из слагаемых в Un,
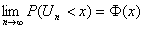
для любого х.
Условия,
о которых идет речь, не будем здесь формулировать. Их можно найти в специальной
литературе (см., например, [6]). «Выяснение условий, при которых действует ЦПТ,
составляет заслугу выдающихся русских ученых А.А.Маркова (1857-1922) и, в
особенности, А.М.Ляпунова (1857-1918)» [9, с.197].
Центральная
предельная теорема показывает, что в случае, когда результат измерения
(наблюдения) складывается под действием многих причин, причем каждая из них
вносит лишь малый вклад, а совокупный итог определяется аддитивно, т.е.
путем сложения, то распределение результата измерения (наблюдения) близко к
нормальному.
Иногда
считают, что для нормальности распределения достаточно того, что результат
измерения (наблюдения) Х формируется под действием многих причин, каждая
из которых оказывает малое воздействие. Это заключение неверно. Важно,
как эти причины действуют. Если аддитивно – то Х имеет приближенно
нормальное распределение. Если мультипликативно (т.е. действия отдельных
причин перемножаются, а не складываются), то распределение Х близко не к
нормальному, а к т.н. логарифмически нормальному, т.е. не Х, а lg X имеет приблизительно нормальное
распределение. Если же нет оснований считать, что действует один из этих двух
механизмов формирования итогового результата (или какой-либо иной вполне
определенный механизм), то про распределение Х ничего определенного
сказать нельзя.
Из
сказанного вытекает, что в конкретной прикладной задаче нормальность
результатов измерений (наблюдений), как правило, нельзя установить из общих
соображений, ее следует проверять с помощью статистических критериев. Или же
использовать непараметрические статистические методы, не опирающиеся на
предположения о принадлежности функций распределения результатов измерений (наблюдений) к тому или иному
параметрическому семейству.

