11.4. Методы размножения выборок (бутстреп-методы)
Эконометрика и прикладная
статистика бурно развиваются последние десятилетия. Серьезным (хотя,
разумеется, не единственным и не главным) стимулом является стремительно
растущая производительность вычислительных средств. Поэтому понятен острый
интерес к статистическим методам, интенсивно использующим компьютеры. Одним из
таких методов является так называемый "бутстреп",
предложенный в 1977 г. Б.Эфроном из Станфордского университета (США).
Сам термин "бутстреп" - это "bootstrap" русскими буквами и
буквально означает что-то вроде: "вытягивание себя (из болота) за шнурки
от ботинок". Термин специально придуман и заставляет вспомнить о подвигах
барона Мюнхгаузена.
В истории эконометрики было несколько
более или менее успешно осуществленных рекламных кампаний. В каждой из них
"раскручивался" тот или иной метод, который, как правило, отвечал
нескольким условиям:
- по мнению его пропагандистов,
полностью решал актуальную научную задачу;
- был понятен (при постановке
задачи, при ее решении и при интерпретации результатов) широким массам
потенциальных пользователей;
- использовал современные
возможности вычислительной техники.
Пропагандисты
метода, как правило, избегали беспристрастного сравнения его возможностей с
возможностями иных эконометрических методов. Если сравнения и проводились, то с
заведомо слабым "противником".
В нашей
стране в условиях отсутствия систематического эконометрического образования
подобные рекламные кампании находили особо благоприятную почву, поскольку у
большинства затронутых ими специалистов не было достаточных знаний в области
методологии построения эконометрических моделей для того, чтобы составить
самостоятельное квалифицированное мнение.
Речь идет о таких методах как бутстреп,
нейронные сети, метод группового учета аргументов, робастные оценки по Тьюки-Хуберу (см. главу 10), асимптотика пропорционального
роста числа параметров и объема данных и др. Бывают локальные всплески
энтузиазма, например, московские социологи в 1980-х годах пропагандировали так
называемый "детерминационный анализ" -
простой эвристический метод анализа таблиц сопряженности, хотя в Новосибирске в
это время давно уже было разработано продвинутое программное обеспечение
анализа векторов разнотипных признаков (см. главу 8).
Однако даже на фоне всех
остальных рекламных кампаний судьба бутстрепа исключительна. Во-первых, признанный его автор Б. Эфрон с самого начала
признавался, что он ничего принципиально нового не сделал. Его исходная статья
(первая в сборнике [21]) называлась:
"Бутстреп-методы: новый взгляд на методы
складного ножа". Во вторых, сразу появились
статьи и дискуссии в научных изданиях, публикации рекламного характера, и даже
в научно-популярных журналах. Бурные обсуждения на конференциях, спешный выпуск
книг. В 1980-е годы финансовая подоплека всей этой активности, связанная с
выбиванием грантов на научную деятельность, содержание учебных заведений и т.п.
была мало понятна отечественным специалистам.
В чем основная идея группы методов "размножения
выборок", наиболее известным представителем которых является бутстреп?
Пусть дана выборка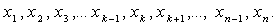 
. В вероятностно-статистической теории предполагаем, что это
- набор независимых одинаково распределенных случайных величин. Пусть
эконометрика интересует некоторая статистика 
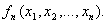Как изучить ее
свойства? Подобными проблемами мы занимались на протяжении всей книги и знаем,
насколько это непросто. Идея, которую предложил в 1949 г. М. Кенуй (это и есть "метод складного ножа") состоит
в том, чтобы из одной выборки сделать много, исключая по одному наблюдению (и возвращая ранее исключенные). Перечислим выборки,
которые получаются из исходной:
;
…
;
…
;
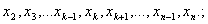
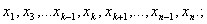
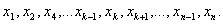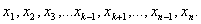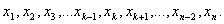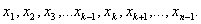
Всего n новых (размноженных) выборок объемом (n-1) каждая. По каждой из них
можно рассчитать значение интересующей эконометрика статистики (с уменьшенным
на 1 объемом выборки):
…
…
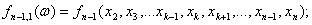
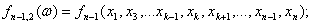
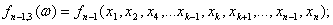
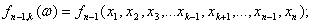
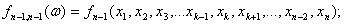
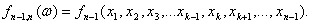
Полученные значения статистики позволяют судить о ее
распределении и о характеристиках распределения - о математическом ожидании,
медиане, квантилях, разбросе, среднем квадратическом отклонении. Значения статистики, построенные по размноженным подвыборкам, не являются независимыми, однако, как мы
видели в главе 5 на примере ряда статистик, возникающих в методе наименьших
квадратов и в кластер-анализе (при обсуждении
возможности объединения двух кластеров), при росте объема выборки влияние
зависимости может ослабевать и со значениями статистик типа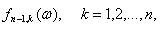 
можно обращаться как с независимыми случайными
величинами.
Однако
и без всякой вероятностно-статистической теории разброс величин 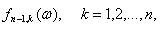дает наглядное
представление о том, какую точность может дать рассматриваемая статистическая
оценка.
Сам М. Кенуй и его последователи использовали размножение выборок
в основном для построения оценок с уменьшенным смещением. А вот Б. Эфрон преложил новый способ размножения выборок, существенно
использующий датчики псевдослучайных чисел. А именно, он предложил строить
новые выборки, моделируя выборки из эмпирического распределения (см.
определения в терминологическом Приложении 1 в конце книги). Другими словами,
Б. Эфрон предложил взять конечную совокупность из n элементов исходной выборки 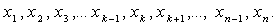и с помощью датчика случайных чисел
сформировать из нее любое число размноженных выборок. Процедура, хотя и
нереальна без ЭВМ, проста с точки зрения программирования. По сравнению с
описанной выше процедурой появляются новые недостатки - неизбежные совпадения
элементов размноженных выборок и зависимость от качества датчиков
псевдослучайных чисел (см. выше). Однако существует математическая теория,
позволяющая (при некоторых предположениях и безграничном росте объема выборки)
обосновать процедуры бутстрепа (см. сборник статей [21]).
Есть
много способов развития идеи размножения выборок (см., например, статью [22]). Можно по
исходной выборке построить эмпирическую функцию распределения, а затем
каким-либо образом от кусочно-постоянной функции перейти к непрерывной функции
распределения, например, соединив точки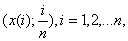 
отрезками прямых.
Другой вариант - перейти к непрерывному распределению, построив
непараметрическую оценку плотности. После этого рекомендуется брать
размноженные выборки из этого непрерывного распределения (являющегося
состоятельной оценкой исходного), непрерывность защитит от совпадений элементов
в этих выборках.
Другой
вариант построения размноженных выборок - более прямой. Исходные данные не
могут быть определены совершенно точно и однозначно. Поэтому предлагается к
исходным данным добавлять малые независимые одинаково распределенные
погрешности. При таком подходе одновременно соединяем вместе идеи устойчивости
(см. главу 10) и бутстрепа. При внимательном анализе
многие идеи эконометрики тесно друг с другом связаны (см. статью [22]).
В каких
случаях целесообразно применять бутстреп, а в каких -
другие эконометрические методы? В период рекламной кампании встречались, в том
числе в научно-популярных журналах, утверждения о том, что и для оценивания
математического ожидания полезен бутстреп. Как
показано в статье [22], это совершенно не
так. При росте числа испытаний методом Монте-Карло бутстреп-оценка приближается к классической оценке -
среднему арифметическому результатов наблюдений. Другими словами, бутстреп-оценка отличается от классической только шумом псевдослучайных чисел.
Аналогичной является ситуация и в
ряде других случаев. Там, где эконометрическая теория хорошо развита, где
найдены методы анализа данных, в том или иной смысле близкие к оптимальным, бутстрепу делать нечего. А вот в новых
областях со сложными алгоритмами, свойства которых недостаточно ясны, он
представляет собой ценный инструмент для изучения ситуации.
