Часть
3. Методы прикладной статистики
3.5. Статистика интервальных
данных
3.5.8. Место статистики
интервальных данных (СИД) в прикладной статистике
Кратко
рассмотрим положение статистики интервальных данных среди других методов
описания неопределенностей и анализа данных.
Нечеткость
и СИД. С формальной точки зрения описание нечеткости интервалом – это
частный случай описания ее нечетким множеством. В СИД функция принадлежности
нечеткого множества имеет специфический вид – она равна 1 в некотором интервале
и 0 вне его. Такая функция принадлежности описывается всего двумя параметрами
(границами интервала). Эта простота описания делает математический аппарат СИД
гораздо более прозрачным, чем аппарат теории нечеткости в общем случае. Это, в
свою очередь, позволяет продвинуться дальше, чем при использовании функций
принадлежности произвольного вида.
Интервальная
математика и СИД. Можно было бы сказать, что СИД – часть интервальной
математики, что СИД так соотносится с прикладной математической статистикой,
как интервальная математика – с математикой в целом. Однако исторически
сложилось так, что интервальная математика занимается прежде всего
вычислительным погрешностями. С точки зрения интервальной математики две
формулы для выборочной дисперсии, рассмотренные выше, имеют разные погрешности.
А с точки зрения СИД эти две формулы задают одну и ту же функцию, и поэтому им
соответствуют совпадающие нотны и рациональные объемы выборок. Интервальная
математика прослеживает процесс вычислений, СИД этим не занимается. Необходимо
отметить, что типовые постановки СИД могут быть перенесены в другие области
математики, и, наоборот, вычислительные алгоритмы прикладной математической
статистики и СИД заслуживают изучения. Однако и то, и другое – скорее дело
будущего. Из уже сделанного отметим применение методов СИД при анализе такой
характеристики финансовых потоков, как NPV – чистая текущая стоимость
[27].
Математическая
статистика и СИД. Как уже отмечалось, математическая статистика и
СИД отличаются тем, в каком порядке делаются предельные переходы 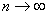 и
и 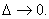 При этом
СИД переходит в математическую статистику при
При этом
СИД переходит в математическую статистику при 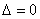 . Правда, тогда исчезают основные особенности
СИД: нотна становится равной 0, а рациональный объем выборки – бесконечности.
Рассмотренные выше методы СИД разработаны в предположении, что погрешности малы
(но не исчезают) и объем выборки велик. СИД расширяет классическую
математическую статистику тем, что в исходных статистических данных каждое
число заменяет интервалом. С другой стороны, можно считать СИД новым этапом
развития математической статистики.
. Правда, тогда исчезают основные особенности
СИД: нотна становится равной 0, а рациональный объем выборки – бесконечности.
Рассмотренные выше методы СИД разработаны в предположении, что погрешности малы
(но не исчезают) и объем выборки велик. СИД расширяет классическую
математическую статистику тем, что в исходных статистических данных каждое
число заменяет интервалом. С другой стороны, можно считать СИД новым этапом
развития математической статистики.
Статистика
объектов нечисловой природы и СИД. Статистика объектов нечисловой
природы (СОНП) расширяет область применения классической математической
статистики путем включения в нее новых видов статистических данных [27].
Естественно, при этом появляются новые виды алгоритмов анализа статистических
данных и новый математический аппарат (в частности, происходит переход от
методов суммирования к методам оптимизации). С точки зрения СОНП частному виду
новых статистических данных – интервальным данным – соответствует СИД.
Напомним, что одно из двух основных понятий СИД – нотна – определяется как
решение оптимизационной задачи. Однако СИД, изучая классические методы
прикладной статистики применительно к интервальным данным, по математическому
аппарату ближе к классике, чем другие части СОНП, например, статистика бинарных
отношений.
Робастные
методы статистики и СИД. Если понимать робастность согласно [3] как
теорию устойчивости статистических методов по отношению к допустимым
отклонениям исходных данных и предпосылок модели, то в СИД рассматривается одна
из естественных постановок робастности. Однако в массовом сознании специалистов
термин «робастность» закрепился за моделью засорения выборки большими выбросами
(модель Тьюки-Хубера), хотя эта модель не имеет большого практического значения
[27]. К этой модели СИД не имеет отношения.
Теория
устойчивости и СИД. Общей схеме устойчивости [3] математических
моделей социально-экономических явлений и процессов по отношению к допустимым
отклонениям исходных данных и предпосылок моделей СИД полностью соответствует.
Он посвящен математико-статистическим моделям, используемым при анализе
статистических данных, а допустимые отклонения – это интервалы, заданные
ограничениями на погрешности. СИД можно рассматривать как пример теории, в
которой учет устойчивости позволил сделать нетривиальные выводы. Отметим, что с
точки зрения общей схемы устойчивости [3] устойчивость по Ляпунову в теории
дифференциальных уравнений – весьма частный случай, в котором из-за его
конкретности удалось весьма далеко продвинуться.
Минимаксные
методы, типовые отклонения и СИД. Постановки СИД относятся к
минимаксным. За основу берется максимально возможное отклонение. Это – подход
пессимиста, используемый, например, в теории антагонистических игр.
Использование минимаксного подхода позволяет подозревать СИД в завышении роли
погрешностей измерения. Однако примеры изучения вероятностно-статистических
моделей погрешностей, проведенные, в частности, при разработке методов
оценивания параметров гамма-распределения [4], показали, что это подозрение не
подтверждается. Влияние погрешностей измерений по порядку такое же, только
вместо максимально возможного отклонения (нотны) приходится рассматривать
математическое ожидание соответствующего отклонения (см. выше). Подчеркнем, что
применение в СИД вероятностно-статистических моделей погрешностей не менее
перспективно, чем минимаксных.
Подход
научной школы А.П. Вощинина и СИД. Если в математической
статистике неопределенность только статистическая, то в научной школе А.П.
Вощинина - только интервальная. Можно сказать, что СИД лежит между классической
прикладной математической статистикой и областью исследований научной школы
А.П. Вощинина. Другое отличие состоит в том, что в этой школе разрабатывают
новые методы анализа интервальных данных, а в СИД в настоящее время изучается
устойчивость классических статистических методов по отношению к малым
погрешностям. Подход СИД оправдывается распространенностью этих методов, однако
в дальнейшем следует переходить к разработке новых методов, специально
предназначенных для анализа интервальных данных.
Анализ
чувствительности и СИД. При анализе чувствительности, как и в СИД,
рассчитывают производные по используемым переменным, или непосредственно
находят изменения при отклонении переменной на +10% от базового
значения. Однако этот анализ делают по каждой переменной отдельно. В СИД все
переменные рассматриваются совместно, и находится максимально возможное
отклонение (нотна). При малых погрешностях удается на основе главного члена
разложения функции в многомерный ряд Тейлора получить удобную формулу для
нотны. Можно сказать, что СИД – это многомерный анализ чувствительности.

