Часть
3. Методы прикладной статистики
3.5. Статистика интервальных
данных
3.5.5. Интервальный
дискриминантный анализ
Перейдем
к задачам классификации в статистике интервальных данных. Как известно [27],
важная их часть – задачи дискриминации (диагностики, распознавания образов с
учителем). В этих задачах заданы классы (полностью или частично, с помощью
обучающих выборок), и необходимо принять решение –к какому этих классов отнести
вновь поступающий объект.
В
линейном дискриминантном анализе правило принятия решений основано на линейной
функции f(x) от
распознаваемого вектора 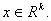 Рассмотрим для простоты случай двух классов.
Правило принятия решений определяется константой С – при f(x)>C распознаваемый объект относится к первому
классу, при f(x)<C – ко
второму.
Рассмотрим для простоты случай двух классов.
Правило принятия решений определяется константой С – при f(x)>C распознаваемый объект относится к первому
классу, при f(x)<C – ко
второму.
В
первоначальной вероятностной модели Р.Фишера предполагается, что классы заданы
обучающими выборками объемов N1 и N2 соответственно из многомерных нормальных распределений с разными
математическими ожиданиями, но одинаковыми ковариационными матрицами. В
соответствии с леммой Неймана-Пирсона, дающей правило принятия решений при
поверке статистических гипотез, дискриминантная функция является линейной. Для
ее практического использования теоретические характеристики распределения
необходимо заменить на выборочные. Тогда дискриминантная функция приобретает
следующий вид
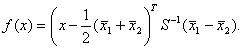
Здесь 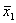 -
выборочное среднее арифметическое по первой выборке
-
выборочное среднее арифметическое по первой выборке 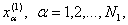 а
а 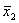 -
выборочное среднее арифметическое по второй выборке
-
выборочное среднее арифметическое по второй выборке 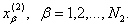 В роли S может выступать любая состоятельная оценка
общей для выборок ковариационной матрицы. Обычно используют следующую оценку,
естественным образом сконструированную на основе выборочных ковариационных
матриц:
В роли S может выступать любая состоятельная оценка
общей для выборок ковариационной матрицы. Обычно используют следующую оценку,
естественным образом сконструированную на основе выборочных ковариационных
матриц:
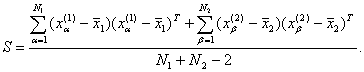
В
соответствии с подходом статистики интервальных данных считаем, что специалисту
по анализу данных известны лишь значения с погрешностями
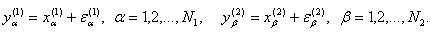
Таким образом, вместо f(x) статистик делает выводы на основе искаженной линейной дискриминантной функции f1(x), в
которой коэффициенты рассчитаны не по исходным данным 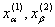 , а по искаженным погрешностями значениям
, а по искаженным погрешностями значениям 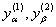 .
.
Это
– модель с искаженными параметрами дискриминантной функции. Следующая модель –
такая, в которой распознаваемый вектор x также известен с ошибкой. Далее, константа С может появляться в модели различными способами. Она может задаваться
априори абсолютно точно. Может задаваться с какой-то ошибкой, не связанной с
ошибками, вызванными конечностью обучающих выборок. Может рассчитываться по
обучающим выборкам, например, с целью уравнять ошибки классификации, т.е.
провести плоскость дискриминации через середину отрезка, соединяющего центры
классов. Итак – целый спектр моделей ошибок.
На
какие статистические процедуры влияют ошибки в исходных данных? Здесь тоже
много постановок. Можно изучать влияние погрешностей измерений на значения
дискриминантной функции f,
например, в той точке, куда попадает вновь поступающий объект х.
Очевидно, случайная величина f(x) имеет
некоторое распределение, определяемое распределениями обучающих выборок. Выше
описана модель Р.Фишера с нормально распределенными совокупностями. Однако
реальные данные, как правило, не подчиняются нормальному распределению [27].
Тем не менее линейный статистический анализ имеет смысл и для распределений, не
являющихся нормальными (при этом вместо свойств многомерного нормального
распределения приходится опираться на многомерную центральную предельную
теорему и теорему о наследовании сходимости [3]). В частности, приравняв
метрологическую ошибку, вызванную погрешностями исходных данных, и
статистическую ошибку, получим условие, определяющее рациональность объемов
выборок. Здесь два объема выборок, а не один, как в большинстве рассмотренных
постановок статистики интервальных данных. С подобным мы сталкивались ранее при
рассмотрении двухвыборочного критерия Смирнова.
Естественно
изучать влияние погрешностей исходных данных не при конкретном х, а для
правила принятия решений в целом. Может представлять интерес изучение
характеристик этого правила по всем х или по какому-либо отрезку. Более
интересно рассмотреть показатель качества классификации, связанный с пересчетом
на модель линейного дискриминантного анализа [27].
Математический
аппарат изучения перечисленных моделей развит выше в предыдущих пунктах
настоящей главы. Некоторые результаты приведены в [14]. Из-за большого объема
выкладок ограничимся приведенными здесь замечаниями.

