|
А.И.
Орлов
Теория принятия решений
Учебное пособие. - М.: Издательство "Март", 2004.
2. ОПИСАНИЕ НЕОПРЕДЕЛЕННОСТЕЙ В ТЕОРИИ ПРИНЯТИЯ РЕШЕНИЙ
2.3.6. Интервальные данные в задачах проверки гипотез
С позиций статистики интервальных данных целесообразно изучить
все практически используемые процедуры прикладной математической статистики,
установить соответствующие нотны и рациональные объемы
выборок. Это позволит устранить разрыв между математическими схемами прикладной
статистики и реальностью влияния погрешностей наблюдений на свойства статистических
процедур. Статистика интервальных данных – часть теории устойчивых статистических
процедур, развитой в монографии [3]. Часть, более адекватная реальной статистической
практике, чем некоторые другие постановки, например, с засорением нормального
распределения большими выбросами.
Рассмотрим подходы статистики интервальных данных в задачах
проверки статистических гипотез. Пусть принятие решения основано на сравнении
рассчитанного по выборке значения статистики критерия 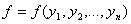 с граничным значением
С: если f>C, то гипотеза отвергается, если же f<C, то принимается.
С учетом погрешностей измерений выборочное значение статистики критерия может
принимать любое значение в интервале с граничным значением
С: если f>C, то гипотеза отвергается, если же f<C, то принимается.
С учетом погрешностей измерений выборочное значение статистики критерия может
принимать любое значение в интервале 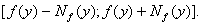 Это означает, что
«истинное» значение порога, соответствующее реально используемому критерию,
находится между C-Nf(y) и C+Nf(y), а потому уровень значимости
описанного правила (критерия) лежит между Это означает, что
«истинное» значение порога, соответствующее реально используемому критерию,
находится между C-Nf(y) и C+Nf(y), а потому уровень значимости
описанного правила (критерия) лежит между 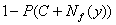 и и 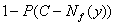 , где P(Z)=P(f<Z). , где P(Z)=P(f<Z).
Пример 1. Пусть 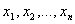 - выборка из нормального
распределения с математическим ожиданием а и единичной дисперсией. Необходимо
проверить гипотезу H0: a = 0 при альтернативе - выборка из нормального
распределения с математическим ожиданием а и единичной дисперсией. Необходимо
проверить гипотезу H0: a = 0 при альтернативе 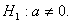
Как известно из любого учебного курса математической статистики,
следует использовать следует использовать статистику 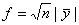 и порог и порог 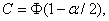 где где 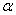 - уровень значимости,
Ф(.) – функция стандартного нормального
распределения с математическим ожиданием 0 и дисперсией 1. В частности, С =
1,96 при - уровень значимости,
Ф(.) – функция стандартного нормального
распределения с математическим ожиданием 0 и дисперсией 1. В частности, С =
1,96 при 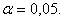
При ограничениях (1) на абсолютную погрешность 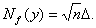 Например, если Например, если
 = 0,1, а n
= 100, то Nf(y) = 1,0. Это означает, что истинное значение порога лежит
между 0,96 и 2,96, а истинный уровень значимости – между 0,003 и 0,34. Можно
сделать и другой вывод: нулевую гипотезу H0 допустимо отклонить на уровне значимости
0,05 лишь тогда, когда f > 2,96. = 0,1, а n
= 100, то Nf(y) = 1,0. Это означает, что истинное значение порога лежит
между 0,96 и 2,96, а истинный уровень значимости – между 0,003 и 0,34. Можно
сделать и другой вывод: нулевую гипотезу H0 допустимо отклонить на уровне значимости
0,05 лишь тогда, когда f > 2,96.
Если же n = 400 при 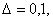 то Nf(y) =2,0 и C-Nf(y) = -0,04, в то время как C+Nf(y) =3,96. Таким образом, даже в случае x = 0 гипотеза H0 может
быть отвергнута только из-за погрешностей измерений результатов наблюдений. то Nf(y) =2,0 и C-Nf(y) = -0,04, в то время как C+Nf(y) =3,96. Таким образом, даже в случае x = 0 гипотеза H0 может
быть отвергнута только из-за погрешностей измерений результатов наблюдений.
Вернемся к общему случаю проверки гипотез. С учетом погрешностей
измерений граничное значение 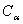 в статистике интервальных
данных целесообразно заменить на в статистике интервальных
данных целесообразно заменить на 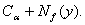 Такая замена дает
гарантию, что вероятность отклонения нулевой гипотезы H0, когда она верна,
не более Такая замена дает
гарантию, что вероятность отклонения нулевой гипотезы H0, когда она верна,
не более 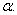 При проверке гипотез
аналогом статистической погрешности, рассмотренной выше в задачах оценивания,
является При проверке гипотез
аналогом статистической погрешности, рассмотренной выше в задачах оценивания,
является 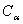 . Суммарная погрешность
имеет вид . Суммарная погрешность
имеет вид 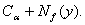 Исходя из принципа
уравнивания погрешностей [3], целесообразно определять рациональный объем выборки
из условия Исходя из принципа
уравнивания погрешностей [3], целесообразно определять рациональный объем выборки
из условия
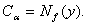
Если f = |f1|, где f1 при справедливости H0 имеет асимптотически
нормальное распределение с математическим ожиданием 0 и дисперсией 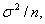 то то
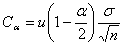 (47) (47)
при больших
n,
где 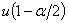 - квантиль порядка - квантиль порядка
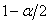 стандартного нормального
распределения с математическим ожиданием 0 и дисперсией 1. Из (47) вытекает,
что в рассматриваемом случае стандартного нормального
распределения с математическим ожиданием 0 и дисперсией 1. Из (47) вытекает,
что в рассматриваемом случае
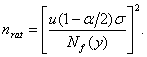
В условиях примера 1 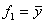 и и
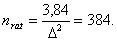
Пример 2. Рассмотрим статистику одновыборочного
критерия Стьюдента
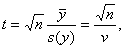
где v – выборочный коэффициент вариации.
Тогда с точностью до бесконечно малых более высокого
порядка нотна для t имеет вид
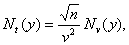
где Nv(y) – рассмотренная ранее нотна для выборочного коэффициента вариации. Поскольку распределение
статистики Стьюдента t сходится к стандартному
нормальному, то небольшое изменение предыдущих рассуждений дает

Пример 3. Рассмотрим двухвыборочный
критерий Смирнова, предназначенный для проверки однородности (совпадения) функций
распределения двух независимых выборок [41]. Статистика этого критерия имеет
вид

где Fm(x) – эмпирическая функция распределения, построенная по
первой выборке объема m, извлеченной из генеральной совокупности с функцией
распределения F(x), а Gn(x) – эмпирическая функция распределения, построенная по
второй выборке объема n, извлеченной из генеральной совокупности с функцией распределения
G(x). Нулевая гипотеза имеет вид 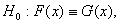 альтернативная
состоит в ее отрицании: альтернативная
состоит в ее отрицании: 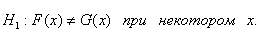 Значение статистики
сравнивают с порогом Значение статистики
сравнивают с порогом 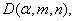 зависящим от уровня
значимости зависящим от уровня
значимости 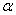 и объемов выборок
m и n. Если значение статистики
не превосходит порога, то принимают нулевую гипотезу, если больше порога – альтернативную.
Пороговые значения и объемов выборок
m и n. Если значение статистики
не превосходит порога, то принимают нулевую гипотезу, если больше порога – альтернативную.
Пороговые значения  берут из таблиц
[42]. Описанный критерий иногда неправильно называют критерием Колмогорова-Смирнова.
История вопроса описана в [43]. берут из таблиц
[42]. Описанный критерий иногда неправильно называют критерием Колмогорова-Смирнова.
История вопроса описана в [43].
При ограничениях (1) на абсолютные погрешности и справедливости
нулевой гипотезы 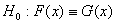 нотна
имеет вид (при больших объемах выборок) нотна
имеет вид (при больших объемах выборок)

Если F(x)=G(x)=x при 0<x<1, то 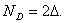 С помощью условия С помощью условия
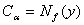 при уровне значимости при уровне значимости
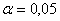 и достаточно больших
объемах выборок (т.е. используя асимптотическое выражение для порога согласно
[42]) получаем, что выборки имеет смысл увеличивать, если и достаточно больших
объемах выборок (т.е. используя асимптотическое выражение для порога согласно
[42]) получаем, что выборки имеет смысл увеличивать, если
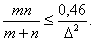
Правая часть этой формулы при 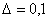 равна 46. Если
m = n, то последнее неравенство переходит
в n < 92. равна 46. Если
m = n, то последнее неравенство переходит
в n < 92.
Теоретические результаты в области статистических методов
входят в практику через алгоритмы расчетов, воплощенные в программные средства
(пакеты программ, диалоговые системы). Ввод данных в современном
статистической программной системе должен содержать запросы о погрешностях результатов
измерений. На основе ответов на эти запросы вычисляются нотны рассматриваемых статистик, а затем – доверительные интервалы
при оценивании, разброс уровней значимости при проверке гипотез, рациональные
объемы выборок. Необходимо использовать систему алгоритмов и программ статистики
интервальных данных, «параллельную» подобным системам для классической математической
статистики.
Материал предоставлен сайтом AUP.Ru (Электронная библиотека экономической и деловой литературы)
Похожие материалы:
Интервальные данные в задачах проверки
гипотез
Теория принятия решений: Интервальные данные в задачах оценивания характеристик распределения
Интервальные данные в задачах оценивания характеристик и параметров распределения
Интервальный
дискриминантный анализ
Прикладная статистика: Интервальный
кластер-анализ
Интервальный дискриминантный анализ
|

