Глава 2. Статистические методы в пространствах произвольной природы

2.6. Статистики интегрального типа

          В прикладной статистике широко используются статистики типа омега-квадрат и типа Колмогорова-Смирнова [6]. Они применяются для проверки согласия с фиксированным распределением или семейством распределений, для проверки однородности двух выборок, симметрии распределения относительно 0, при оценивании условной плотности и регрессии в пространствах произвольной природы и т.д.

          Статистики интегрального типа и их асимптотика. Рассмотрим статистики интегрального типа

,                   (1)

где Х – некоторое пространство, по которому происходит интегрирование (например, X = [0; 1], X = R¹ или X = R^k). Здесь {α} – направленное множество, переход к пределу по которому обозначен как α→∞ (см. приложение 1). Случайные функции f_α: XЧΩ → Y обычно принимают значения, являющиеся числами. Но иногда рассматривают и постановки, в которых У = R^k или У – банахово пространство (т.е. полное нормированное пространство [27]). Наконец, F_α(x,ω) – случайная функция распределения или случайная вероятностная мера; в последнем случае используют также обозначение dF_α(x,ω)= F_α(dx,ω).

          Предполагаются выполненными необходимые для корректности изложения внутриматематические предположения измеримости, например, сформулированные в [28, 29].

          Пример 1. Рассмотрим критерий Лемана – Розенблатта, т.е. критерий типа омега-квадрат для проверки однородности двух независимых выборок [6]. Его статистика имеет вид:

LR = 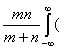F_m(x) – G_n(x))²dH_m+n(x) ,

где F_m(x) – эмпирическая функция распределения, построенная по первой выборке объема m, G_n(x)) - эмпирическая функция распределения, построенная по второй выборке объема n, а H_m+n(x) – эмпирическая функция распределения, построенная по объединенной выборке объема m+n. Легко видеть, что

H_m+n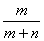(x) = F_m(x) + 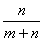G_n(x).

          Ясно, что статистика LR имеет вид (1). При этом х – действительное число, Х = У = R¹, в роли α выступает пара (m, n), и α→∞ означает, что min(m, n) → ∞. Далее,

f_α(x,ω) =.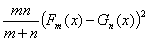

Наконец, F_α(x,ω) = H_m+n(x).

          Теперь обсудим асимптотическое поведение функций f_α(x,ω) и F_α(x,ω), с помощью которых определяется статистика Лемана – Розенблатта LR. Ограничимся случаем, когда справедлива гипотеза однородности, т.е. совпадают функции распределения, соответствующие генеральным совокупностям, из которых взяты выборки. Их общую функцию распределения обозначим F(x). Она предполагается непрерывной. Введем в рассмотрение выборочные процессы

.

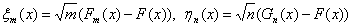Нетрудно проверить, что

.

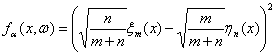          Сделаем замену переменной t = F(x). Тогда выборочные процессы переходят в соответствующие эмпирические процессы (см. приложение 1):

.

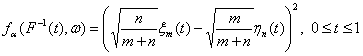Конечномерные распределения этого процесса, т.е. распределения случайных векторов

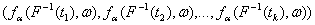
для всех возможных наборов (t₁, t₂, … , t_k), сходятся к конечномерным распределениям квадрата броуновского моста ξ²(t). В соответствии с разделом П-5 приложения 1 рассматриваемая сходимость по распределению обозначается так:

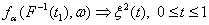.               (2)

          Нетрудно видеть, что при любом х

F_α(x,ω) = H_m+n(x) → F(x)

при α→∞ (сходимость по вероятности). С помощью замены переменной t = F(x) получаем, что

F_α(F^-1(t),ω) = H_m+n(F^-1(t)) → t            (3)

при α→∞. Из соотношений (2) и (3) хотелось бы сделать вывод, что в случае статистики Лемана - Розенблатта типа омега-квадрат

,

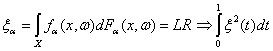т.е. предельным распределением этой статистики является классическое распределение [30], найденное как предельное для одновыборочной статистики критерия согласия омега-квадрат, известного также как критерий Крамера - Мизеса - Смирнова.

          Действительно, сформулированное утверждение справедливо. Однако доказательство нетривиально.

          Так, может показаться очевидным следующее утверждение.

          Утверждение 1. Пусть f: [0; 1] → R¹ – ограниченная функция, G_n(x) и G(x) – функции распределения, G_n(0) = G(0) =0, G_n(1) = G(1) = 1, причем G_n(x) → G(x) при всех х. Тогда

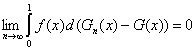.                  (4)

          Это утверждение неверно (ср. [31, с.42]). Действительно, пусть f(x) = 1, если х рационально, и f(x) = 0, если х иррационально, G(x) =x, а G_n(x) имеет скачки величиной 2^-n в точках m/2ⁿ, m = 1, 2, … , 2ⁿ при всех n =1, 2, … Тогда G_n(x) → G(x) при всех х, однако

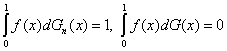
при всех n =1, 2, … Следовательно, вопреки сформулированному выше утверждению 1,

,

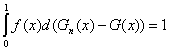т.е. соотношение (4) неверно.

          Итак, сформулируем проблему. Пусть известно, что последовательность случайных функций f_α(x, ω) сходится по распределению при α→∞ к случайной функции f(x,ω). Пусть последовательность случайных мер F_α(A,ω), определенных на множествах А из достаточно обширного семейства, сходится по распределению к вероятностной мере F(A) при α→∞. Если речь идет о конечномерном пространстве и меры задаются функциями распределения, то сходимость F_α(х,ω) к F(х) должна иметь место во всех точках непрерывности F(х). В каких случаях можно утверждать, что при α→∞ справедлив предельный переход    

?

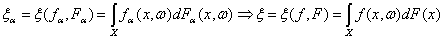Выше показано, что, например, ограниченности f_α(x, ω) для этого недостаточно.

          Метод аппроксимации ступенчатыми функциями. Рассмотрим общий метод, позволяющий получить предельные распределения не только для статистик интегрального типа, но и для других статистических критериев, например, для критериев типа Колмогорова. Пусть T = {С₁, С₂, … , С_k} – разбиение пространства Х на непересекающиеся подмножества. Пусть в каждом элементе С_j разбиения T выделена точка x_j, j = 1, 2, … , k. На множестве функций f: X → Y введем оператор A_T: если xС_j, то

A_Tf(x) = f(x_j), j = 1, 2, … . k.               (5)

Тогда A_Tf – аппроксимация функции f ступенчатыми (кусочно-постоянными) функциями.

          Пусть f_α(x,ω) – последовательность случайных функций на Х, а К(∙) – функционал на множестве всех возможных их траекторий как функций от х. Для изучения распределения К(f_α) методом аппроксимации ступенчатыми функциями используют разложение

К(f_α) = К(А_Тf_α) + {К(f_α) - К(А_Тf_α)}.               (6)

Согласно (5) распределение первого слагаемого в (6) определяется конечномерным распределением случайного элемента, а именно, распределением вектора

(f_α(x₁,ω), f_α(x₂,ω), …  f_α(x_k,ω)).           (7)

          В обычных постановках предельной теории классических непараметрических критериев распределение вектора (7) сходится при α→∞ к соответствующему конечномерному распределению предельной случайной функции f(x,ω), т.е. к распределению случайного вектора

(f(x₁,ω), f(x₂,ω), …  f(x_k,ω)).               (8)

В соответствии с теорией наследования сходимости (приложение 1) при слабых условиях на функционал К(∙) из сходимости по распределению вектора (7) к вектору (8) следует сходимость по распределению К(А_Тf_α) к К(А_Тf).

          Используя аналогичное (6) разложение

К(f) = К(А_Тf) + {К(f) - К(А_Тf)},          (9)

можно устанавливать сходимость по распределению К(f_α) к К(f) при α→∞ в два этапа: сначала выбрать разбиение Т так, чтобы вторые слагаемые в правых частях соотношений (6) и (9) были малы, а затем при фиксированном операторе А_Т воспользоваться сходимостью по распределению К(А_Тf_α) к К(А_Тf).

          Рассмотрим простой пример применения метода аппроксимации ступенчатыми функциями.

          Обобщение теоремы Хелли. Пусть f: [0; 1] → R¹ – измеримая функция, F_n(x) – функции распределений, сосредоточенных на отрезке [0; 1]. Пусть F_n(x) сходятся в основном к функции распределения F(x), т.е.

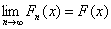                (10)

для всех х, являющихся точками непрерывности F(x).

          Утверждение 2. Если f(x) – непрерывная функция, то

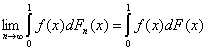                (11)

(рассматриваются интегралы Лебега-Стилтьеса).

          Утверждение 2 известно в литературе как первая теорема Хелли [27, с.344-346], вторая теорема Хелли [32, с.174-175], лемма Хелли-Брея [33, с.193-194].

          Естественно поставить вопрос: при каких f из (10) следует (11)? Необходимо ввести условия и на F_n: если F_n ≡ F, то соотношение (11) верно для любой измеримой функции f, для которой интеграл в (11) существует. Поэтому рассмотрим следующую постановку.

          Постановка 1. Пусть функция f такова, что для любой последовательности F_n, удовлетворяющей (10), справедливо (11). Что можно сказать о функции f?

          В работах [28, 29] найдены следующие необходимые и достаточные условия на функцию f.

          Теорема 1. Пусть ограниченная на [0; 1] функция f интегрируема по Риману-Стилтьесу по функции распределения F(x). Тогда для любой последовательности функций распределения F_n, сходящейся в основном к F, имеет место предельный переход (11).

          Теорема 2. Пусть функция f не интегрируема по Риману-Стилтьесу по функции распределения F(x). Тогда существует последовательность функций распределения F_n, сходящаяся в основном к F, для которой соотношение (11) не выполнено.

          Теоремы 1 и 2 в совокупности дают необходимые и достаточные условия для f в постановке 1. А именно, необходимо и достаточно, чтобы ограниченная на [0; 1] функция f была интегрируема по Риману-Стилтьесу по F.

          Напомним определение интегрируемости функции f по Риману-Стилтьесу по функции распределения F [27, с.341]. Рассмотрим разбиение T = {С₁, С₂, … , С_k}, где

С_i = [y_i-1, y_i), i = 1, 2, …, m – 1, С_m = [y_m-1, y_m],     (12)

0 = y₀ < y₁ < y₂ <…< y_m = 1.

Выберем в С_i произвольную точку x_i, i = 1, 2, …, m, и составим сумму

.

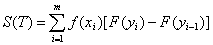Если при max(y_i – y_i-1) → 0 эти суммы стремятся к некоторому пределу (не зависящему ни от способа дробления отрезка [0; 1], ни от выбора точек x_i  в каждом из элементов разбиения), то этот предел называется интегралом Римана-Стилтьеса от функции f по функции F по отрезку [0; 1] и обозначается символом, приведенным в правой части равенства (11).

          Рассмотрим суммы Дарбу-Стилтьеса

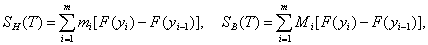
где

.

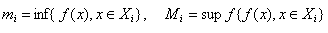Ясно, что

S_H(T) < S(T) < S_B(T).

Необходимым и достаточным условием интегрируемости по Риману-Стилтьесу является следующее: для любой последовательности разбиений T_k, k = 1, 2, 3, … вида (12) такой, что max(y_i – y_i-1) → 0 при k→∞, имеем

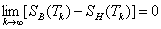.               (13)

          Напомним, что согласно разделу П-3 приложения 1 колебанием δ(f, B) функции f на множестве B называется δ(f, B) = sup{|f(x) – f(y)|, x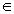B, y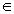B}. Поскольку

δ(f, С_i) = M_i – m_i,

то условие (13) можно записать в виде

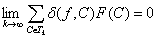.                (14)

Условие (14), допускающее обобщение с Х = [0; 1] и f: [0; 1] → R¹ на X и f более общего вида, и будем использовать при доказательстве теорем 1 и 2.

          Доказательство теоремы 1. Согласно методу аппроксимации ступенчатыми функциями рассмотрим оператор А_Т. Как легко проверить, имеет место разложение

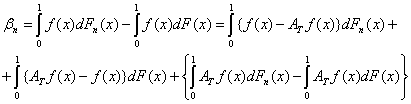.   (15)

          Поскольку

|f(x) - A_Tf(x)| < δ(f, X_i),  x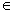С_i,

то первое слагаемое в правой части (15) не превосходит

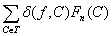,               (16)

а второе не превосходит

.

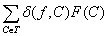Согласно определению оператора А_Т третье слагаемое в (15) имеет вид

.

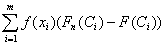Очевидно, оно не превосходит по модулю

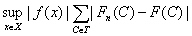
(здесь используется ограниченность f на X).

          Согласно (16) первое слагаемое в правой части (15) не превосходит

.

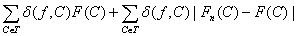Поскольку

,

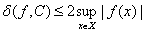то первое слагаемое в правой части (15) не превосходит

.

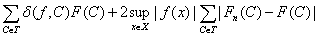          Из оценок, относящихся к трем слагаемым в разложении (15), следует, что

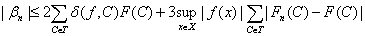.            (17)

          Используя оценку (17), докажем, что β_n → 0 при n → ∞. Пусть дано ε > 0. Согласно условию интегрируемости функции f по Риману-Стилтьесу, т.е. условию (14), можно указать разбиение T = T(ε) такое, что

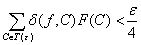,                   (18)

и в точках y_i, i = 1, 2, …, m - 1 (см. (12)), функция F непрерывна.

          Поскольку

F_n(X_i) = F_n(y_i) - F_n(y_i-1),

то из (10) следует, что существует число n = n(ε) такое, что при n > n(ε) справедливо неравенство

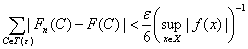.       (19)

Из (17), (18) и (19) следует, что при n > n(ε) справедливо неравенство

,

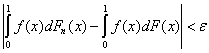что и требовалось доказать.

          Обсудим условие ограниченности f. Если оно не выполнено, то из (10) не всегда следует (11).

          Пример 2. Пусть f(x) = 1/x при x > 0 и f(0)=0. Пусть F(0,5) = 0, т.е. предельное распределение сосредоточено на [1/2; 1]. Пусть распределение F_n на [0; Ѕ) имеет единственный атом в точке x = 1/n величиной n^-1/2, а на [1/2; 1] справедливо (10). Тогда по причинам, изложенным при доказательстве теоремы 1,

,

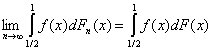однако

,

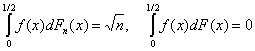т.е. соотношение (11) не выполнено.

          Условие ограниченности подынтегральной функции f можно заменить, как это сделано, например, в [28], на условие строгого возрастания функции распределения F.

          Лемма. Пусть функции распределения F всюду строго возрастает, т.е. из x₁ < x₂ вытекает F(x₁) < F(x₂). Пусть функция f интегрируема по Риману-Стилтьесу по F, т.е. выполнено (14). Тогда функция f ограничена.

          Доказательство. Рассмотрим точки 0 = y₀ < y₁ < y₂ <…< y_2m = 1 и два разбиения

.

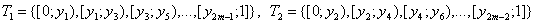Тогда для любых двух точек х и х′ можно указать конечную последовательность точек x₁ = x, x₂, x₃, …, x_s, x_s+1 = x′ такую, что любые две соседние точки x_i, x_i+1, i = 1, 2, …, s, одновременно принадлежат некоторому элементу C_i разбиения T₁ или разбиения T₂, причем С_i ≠ С_j при i ≠ j. Действительно, пусть . Пусть для определенности q > p. Тогда можно положить x₂ = y_p+1, x₃ = y_p+2, …, x_s = y_q. Поскольку среди элементов разбиений Т₁ и Т₂ есть С₁ = [y_p; y_p+2), то 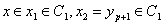. Далее, 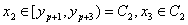, и т.д.

          Из указанных выше свойств последовательности x₁ = x, x₂, x₃, …, x_s, x_s+1 = x′ следует, что

.

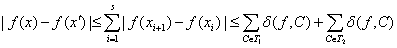Пусть теперь число max(y_i – y_i-2) настолько мало, что согласно (14)

.

Тогда согласно двум последним соотношениям

,

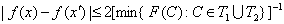что и доказывает лемму.

          Доказательство теоремы 2. Пусть условие (14) не выполнено, т.е. существуют число γ > 0 и последовательность разбиений T_n, n = 1, 2, …, такие, что max(y_i – y_i-1) → 0 при n→∞ и при всех n

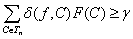.           (20)

Для доказательства теоремы построим две последовательности функций распределения F_1n и F_2n, n = 1, 2, …, для которых выполнено (10), но последовательность

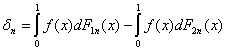
не стремится к 0 при n → ∞. Тогда (11) не выполнено хотя бы для одной из последовательностей F_1n и F_2n.

          Для любого С – элемента некоторого разбиения Т – можно указать, как вытекает из определения δ(f, C), точки x₁(C) и x₂(C) такие, что

f (x₁(C)) - f(x₂(C)) > Ѕ δ(f, C).             (21)

          Построим F_1n и F_2n следующим образом. Пусть F_1n(С) = F_2n(С) = F(С) для любого С из T_n. При этом F_1n имеет в С один атом в точке x₁(C) величиной F(С), а F_2n имеет в С также один атом в точке x₂(C) той же величины F(С). Другими словами, распределение F_1n в С сосредоточено в одной точке, а именно, в x₁(C), а распределение F_2n сосредоточено в x₂(C). Тогда

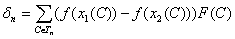.                   (22)

Из (20), (21) и (22) следует, что

.

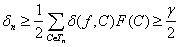          Остается показать, что для последовательностей функций распределения F_1n и F_2n выполнено (10). Пусть х – точка непрерывности F. Пусть

y₁(x, T) = max{y_kn: y_kn < x}, y₂(x, T) = min{ y_kn: y_kn > x},

где y_kn – точки, определяющие разбиения T_n согласно (12). В соответствии с определением F_in

F_in(y_j(x, T_n))= F(y_j(x, T_n)), i = 1, 2, j = 1, 2,

а потому

|F_in(x) – F(x)| < F(y₂(x, T_n)) - F(y₁(x, T_n)), i = 1, 2.

В силу условия max(y_kn – y_(k-1)n) → 0 и непрерывности F в точке x правая часть последнего соотношения стремится к 0 при n → ∞, что и заканчивает доказательство теоремы 2.

          Теоремы 1 и 2 демонстрируют основные идеи предельной теории статистик интегрального типа и непараметрических критериев в целом. Как показывают эти теоремы, основную роль в рассматриваемой теории играет предельное соотношение (14). Отметим, что если δ(f, T_n) → 0 при n → ∞, то (14) справедливо, но, вообще говоря, не наоборот. Естественно возникает еще ряд постановок. Пусть (14) выполнено для f₁ и f₂. При каких функциях h это соотношение выполнено для h(x, f₁(x), f₂(x))? В прикладной статистике вместо f(x) рассматривают f_α(x, ω) и f(x, ω), а вместо интегрирования по функциям распределения F_n(x) – интегрирование по случайным мерам F_α(ω). Как меняются формулировки в связи с такой заменой? В связи со слабой сходимостью (т.е. сходимостью по распределению) A_Tf_α к A_T и переходом от f_α(x, ω) к h_α(x, f_1α(x, ω), f_2α(x, ω)) возникает следующая постановка. Пусть κ_α слабо сходится к κ при α→∞. Когда распределения g_α(κ_α) сближаются с распределениями g_α(κ)? Полным ответом на последний вопрос являются необходимые и достаточные условия наследования сходимости. Они приведены в приложении 1.

          Основные результаты. Наиболее общая теорема типа теоремы 1 выглядит так [29].

          Теорема 3. Пусть существует последовательность разбиений T_n, n = 1, 2, …, такая, что при n →∞ и α→∞

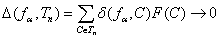.             (23)

Пусть для любого С, входящего хотя бы в одно из разбиений T_n,

F_α(C, ω) → F(C)            (24)

при α→∞ (сходимость по вероятности). Пусть f_α асимптотически ограничены по вероятности при α→∞. Тогда

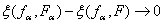               (25)

при α→∞ (сходимость по вероятности).

          Как известно, полное сепарабельное метрическое пространство называется польским. Это понятие понадобится для формулировки аналога теоремы 2.

          Теорема 4. Пусть Х – польское пространство, У конечномерно, существует измельчающаяся последовательность T_n разбиений, для которой соотношение (23) не выполнено. Тогда существует удовлетворяющая (24) последовательность F_α, для которой соотношение (25) неверно, хотя F_α слабо сходится к F при α→∞.

          Условие (23) естественно назвать условием римановости, поскольку в случае, рассмотренном в теореме 1, оно является условием интегрируемости по Риману-Стилтьесу. Рассмотрим наследуемость римановости при переходе от f_1α(x, ω) со значениями в У₁ и f_2α(x, ω) со значениями в У₂, удовлетворяющих (23), к h_α(x, f_1α(x, ω), f_2α(x, ω)) со значениями в У₃.

          Положим

,

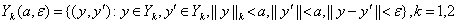где ||∙||_k – норма (т.е. длина вектора) в пространстве Y_k, k = 1, 2. Рассмотрим также множества

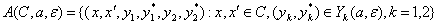
и функции

.

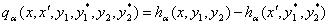Наконец, понадобится измеритель колеблемости

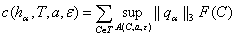
и множество

.

          Теорема 5. Пусть функции h_α асимптотически (при α→∞) ограничены на множестве Z(a) при любом положительном a. Пусть функции f_1α и f_2α асимптотически ограничены по вероятности и удовлетворяют условию (23). Пусть для участвующей в (23) последовательности T_n

c(h_α, T_n, a, ε) → 0          (26)

при α→∞, n→∞, ε→ 0 и любом положительном a. Тогда функции f_3α(x, ω) = h_α(x, f_1α(x, ω), f_2α(x, ω)) удовлетворяют условию (23) и асимптотически ограничены по вероятности.

          Теорема 6. Пусть условие (26) не выполнено для h_α. Тогда существуют детерминированные ограниченные функции f_1α и f_2α такие, что соотношение (23) выполнено для f_1α и f_2α и не выполнено для f_3α.

          Пример 3. Пусть X = [0; 1]^k, пространства Y₁ и Y₂ конечномерны, функция h_α ≡ h(x, y₁, y₂) непрерывна. Тогда условие (26) выполнено.

          С помощью теорем 3 и 5 и результатов о наследовании сходимости можно изучить асимптотическое поведение статистик интегрального типа

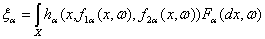
со значениями в банаховом пространстве У.

          Теорема 7. Пусть для некоторой последовательности T_n разбиений Х справедливы соотношения (23) для f_1α и f_2α и (24) для F_α. Пусть последовательность функций h_α удовлетворяет условию в теореме 5, конечномерные распределения (f_1α(x, ω), f_2α(x, ω)) слабо сходятся к конечномерным распределениям (f₁(x, ω), f₂(x, ω)), причем для f₁ и f₂ справедливо соотношение (23). Тогда

,

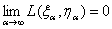где L – расстояние Прохорова (см. раздел П-3 приложения 1),

.

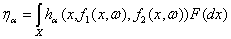          Теорема 7 дает общий метод получения асимптотических распределений статистик интегрального типа. Важно, что соотношение (23) выполнено для эмпирического процесса и для процессов, связанных с оцениванием параметров при проверке согласия [28].

          Один из выводов общей теории состоит в том, что в качестве F_α можно использовать практически любую состоятельную оценку истинной функции распределения. Этот вывод использовался при построении критерия типа омега-квадрат для проверки симметрии распределения относительно 0 и обнаружения различий в связанных выборках (см. ниже).

          Асимптотическое поведение критериев типа Колмогорова может быть получено с помощью описанного выше метода аппроксимации ступенчатыми функциями. Этот метод не требует обращения к теории сходимости вероятностных мер в функциональных пространствах. Для критериев Колмогорова и Смирнова достаточно использовать лишь свойства эмпирического процесса и броуновского моста. В случае проверки согласия добавляется необходимость изучения еще одного  случайного процесса. Он является разностью между двумя функциями распределения. Одна - функция распределения элементов выборки. Вторая - случайный элемент параметрического семейства распределений, полученный путем подстановки оценок параметров вместо их истинных значений.

          Статистика интегрального типа для проверки симметрии распределения. В прикладной статистике часто возникает необходимость проверки гипотезы о симметрии распределения относительно 0. Так, при проверке однородности связанных выборок необходимость проверки этой гипотезы основана на следующем факте [6]. Если случайные величины Х и Y независимы и одинаково распределены, то для функции распределения H(x)=P(Z<x) случайной величины Z = X – Y выполнено, как нетрудно видеть, соотношение

H(-x)=1 - H(x).

          Это соотношение означает симметрию функции распределения относительно 0. Плотность такой функции распределения является четной функцией, ее значения в точках х и (-х) совпадают. Проверка гипотезы однородности связанных выборок в наиболее общем случае сводится к проверке симметрии функции распределения разности Z = X – Y относительно 0.

         Рассмотрим методы проверки этой гипотезы. Сначала обсудим, какого типа отклонения от гипотезы симметрии можно ожидать при альтернативных гипотезах?

          Рассмотрим сначала альтернативу сдвига

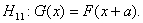
В этом случае распределение Z при альтернативе отличается сдвигом от симметричного относительно 0. Для проверки гипотезы однородности может быть использован критерий знаковых рангов, разработанный Вилкоксоном (см., например, справочник [34, с.46-53]).

          Альтернативная гипотеза общего вида записывается как

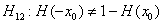
при некотором х₀ . Таким образом, проверке подлежит гипотеза симметрии относительно 0, которую можно переписать в виде

H(x) + H(-x) - 1 = 0 .

Для построенной по выборке Z_j = X_j  - Y_{j ,} j = 1,2,…,n, эмпирической функции распределения H_n(x) последнее соотношение выполнено лишь приближенно:

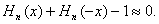
Как измерять отличие от 0? По тем же соображениям, что и в предыдущем пункте, целесообразно использовать статистику типа омега-квадрат. Соответствующий критерий был предложен в работе [35]. Он имеет вид

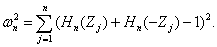             (27)

          Представим эту статистику в интегральном виде. Рассмотрим выборочный процесс

.

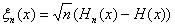При справедливости нулевой гипотезы

.

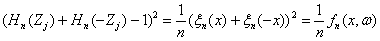Положим

.

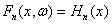Тогда, как легко видеть, статистика, заданная формулой (27), представляется в виде

.

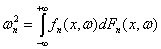Таким образом, асимптотическое поведение этой статистики может быть изучено с помощью описанной выше предельной теории статистик интегрального типа. Исторически ход мысли был обратным - сначала была построена и изучена статистика (27), а потом путем обобщения разработанных при анализе конкретной статистики методов исследования была построена общая теория, включающая в себя ряд необходимых и достаточных условий.

          Критерий проверки гипотезы симметрии распределения относительно 0 с помощью статистики (27) является состоятельным, т.е. если функция распределения элементов выборки не удовлетворяет рассматриваемой гипотезе, то вероятность отклонения гипотезы стремится к 1 при росте объема выборки.

          В работе [35] найдено предельное распределение этой статистики:

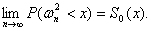
В табл.1 приведены критические значения статистики типа омега-квадрат для проверки симметрии распределения (и тем самым для проверки однородности связанных выборок), соответствующие наиболее распространенным значениям уровней значимости (расчеты проведены Г.В. Мартыновым; см.также [31]).

Таблица 1. Критические значения статистики 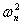 для проверки симметрии распределения

Значение функции распределения	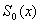Уровень значимости	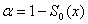Критическое значение х статистики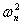
0,90	0,10	1,20
0,95	0,05	1,66
0,99	0,01	2,80

          Как следует из табл.1, правило принятия решений при проверке симметрии распределения (или однородности связанных выборок) в наиболее общей постановке и при уровне значимости 5% формулируется так. Вычислить статистику 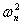. Если 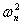<1,66, то принять гипотезу однородности. В противном случае - отвергнуть.

          Пример. Пусть величины Z_{j ,} j=1,2,…,20, таковы:

20, 18, (-2), 34, 25, (-17), 24, 42, 16, 26,

13, (-23), 35, 21, 19, 8, 27, 11, (-5), 7.

Соответствующий вариационный ряд 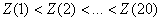имеет вид:

(-23)<(-17)<(-5)<(-2)<7<8<11<13<16<18<

<19<20<21<24<25<26<27<34<35<42.

          Для расчета значения статистики 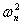 построим табл.2 из 7 столбцов и 20 строк, не считая заголовков столбцов (сказуемого таблицы). В первом столбце указаны номера (ранги) членов вариационного ряда, во втором - сами эти члены, в третьем - значения эмпирической функции распределения при значениях аргумента, совпадающих с членами вариационного ряда. В следующем столбце приведены члены вариационного ряда с обратным знаком, а затем указываются соответствующие значения эмпирической функции распределения. Например, поскольку минимальное наблюдаемое значение равно (-23), то H_n(x) = 0 при x < -23, а потому для членов вариационного ряда с 14-го по 20-й в пятом столбце стоит 0. В качестве другого примера рассмотрим минимальный член вариационного ряда, т.е. (-23). Меняя знак, получаем 23. Это число стоит между 13-м и 14-м членами вариационного ряда, 21<23<24. На этом интервале эмпирическая функция распределения совпадает со своим значением в левом конце, поэтому следует записать в пятом столбце значение 0,65. Остальные ячейки пятого столбца заполняются аналогично. На основе третьего и пятого столбцов элементарно заполняется шестой столбец, а затем и седьмой. Остается найти сумму значений, стоящих в седьмом столбце. Подобная таблица удобна как для ручного счета, так и при использовании электронных таблиц типа Excel.

Таблица 2. Расчет значения статистики 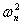 для проверки симметрии распределения

j	Z(j)	Hn(Z(j))	- Z(j)	Hn(-Z(j))	Hn(Z(j))+Hn(-Z(j))-1	(Hn(Z(j))+Hn(-Z(j))-1)2
1	-23	0,05	23	0,65	-0,30	0,09
2	-17	0,10	17	0,45	-0,45	0,2025
3	-5	0,15	5	0,20	-0,65	0,4225
4	-2	0,20	2	0,20	-0,60	0,36
5	7	0,25	-7	0,10	-0,65	0,4225
6	8	0,30	-8	0,10	-0,60	0,36
7	11	0.35	-11	0,10	-0,55	0,3025
8	13	0,40	-13	0,10	-0,50	0,25
9	16	0,45	-16	0,10	-0,45	0,2025
10	18	0,50	-18	0,05	-0,45	0,2025
11	19	0,55	-19	0,05	-0,40	0,16
12	20	0,60	-20	0,05	-0,35	0,1225
13	21	0,65	-21	0,05	-0,30	0,09
14	24	0,70	-24	0	-0,30	0,09
15	25	0,75	-25	0	-0,25	0,0625
16	26	0,80	-26	0	-0,20	0,04
17	27	0,85	-27	0	-0,15	0,0225
18	34	0,90	-34	0	-0,10	0,01
19	35	0,95	-35	0	-0,05	0,0025
20	42	1,00	-42	0	0	0

          Результаты расчетов (суммирование значений по седьмому столбцу табл.2) показывают, что значение статистики 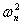=3,055. В соответствии с табл.1 это означает, что на любом используемом в прикладных эконометрических исследованиях уровнях значимости отклоняется гипотеза симметрии распределения относительно 0 (а потому и гипотеза однородности в связанных выборках).