Статистика объектов нечисловой природы

Методы статистики объектов нечисловой природы (статистики нечисловых данных, или нечисловой статистики) применяют всегда, когда результаты наблюдений являются объектами нечисловой природы. Например, сообщениями о годности или дефектности единиц продукции. Информацией о сортности единиц продукции. Разбиениями единиц продукции на группы соответственно значения контролируемых параметров. Упорядочениями единиц продукции по качеству или инвестиционных проектов по предпочтительности. Фотографиями поверхности изделия, пораженной коррозией, и т.д. Итак, объекты нечисловой природы – это измерения по качественному признаку, множества, бинарные отношения (разбиения, упорядочения и др.) и многие другие математические объекты [2]. Они используются в различных вероятностно-статистических методах принятия решений. В частности, в задачах управления качеством продукции, а также, например, в медицине и социологии, как для описания результатов приборных измерений, так и для анализа экспертных оценок.

Для описания данных, являющихся объектами нечисловой природы, применяют, в частности, таблицы сопряженности, а в качестве средних величин – решения оптимизационных задач [2]. В качестве выборочных средних для измерений в порядковой шкале используют медиану и моду, а в шкале наименований – только моду. О методах классификации нечисловых данных говорилось выше.

Для решения параметрических задач оценивания используют оптимизационный подход, метод одношаговых оценок, метод максимального правдоподобия, метод устойчивых оценок. Для решения непараметрических задач оценивания наряду с оптимизационными подходами к оцениванию характеристик используют непараметрические оценки распределения случайного элемента, плотности распределения, функции, выражающей зависимость [2].

В качестве примера методов проверки статистических гипотез для объектов нечисловой природы рассмотрим критерий «хи-квадрат» (обозначают χ²), разработанный К.Пирсоном для проверки гипотезы однородности (другими словами, совпадения) распределений, соответствующих двум независимым выборкам.

Рассматриваются две выборки объемов n₁ и n₂, состоящие из результатов наблюдений качественного признака, имеющего k градаций. Пусть m_1j и m_2j – количества элементов первой и второй выборок соответственно, для которых наблюдается j–я градация, а p_1j и p_2j – вероятности того, что эта градация будет принята, для элементов первой и второй выборок, j = 1, 2, …, k.

Для проверки гипотезы однородности распределений, соответствующих двум независимым выборкам,

H₀: p_1j = p_2j, j = 1, 2, …, k,

применяют критерий χ² (хи-квадрат) со статистикой

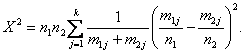
Установлено [9, 11], что статистика Х² при больших объемах выборок n₁ и n₂ имеет асимптотическое распределение хи-квадрат с (k – 1) степенью свободы.

Таблица 1

Распределения плавок стали по процентному содержанию серы

Содержание серы, в %	Число плавок
	Завод А	Завод Б
0,00 ÷ 0,02	82	63
0,02 ÷ 0,04	535	429
0,04 ÷ 0,06	1173	995
0,06 ÷ 0,08	1714	1307

Пример 3. В табл.1 приведены данные о содержании серы в углеродистой стали, выплавляемой двумя металлургическими заводами. Проверим, можно ли считать распределения примеси серы в плавках стали этих двух заводов одинаковыми.

Расчет по данным табл.1 дает Х² = 3,39. Квантиль порядка 0,95 распределения хи-квадрат с k – 1 = 3 степенями свободы равен 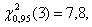 а потому гипотезу о совпадении функций распределения содержания серы в плавках двух заводов нельзя отклонить, т.е. ее следует принять (на уровне значимости α = 0,05).

Выше дано лишь краткое описание содержания прикладной статистики на современном этапе. Подробное изложение конкретных методов содержится в специальной литературе.