Формулы
Байеса
Применим формулу полной вероятности для вывода т.н. «формул
Байеса», которые иногда используют при проверке статистических гипотез.
Требуется найти вероятность события Ai, если известно, что событие В произошло. Согласно теореме умножения
Р(АiВ) = P(B)P(Ai|B) = Р(Аi) Р(В|Ai).
Следовательно,
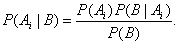
Используя формулу полной вероятности
для знаменателя, находим, что
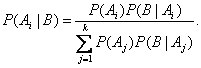
Две
последние формулы и называют обычно формулами Байеса. Общая схема их
использования такова. Пусть событие В может протекать в различных
условиях, относительно которых может быть сделано k гипотез A1, A2,…, Ak. Априорные (от a priori (лат.) – до опыта) вероятности этих
гипотез есть Р(A1), Р(A2),…, Р(Ak). Известно также, что при
справедливости гипотезы Ai вероятность осуществления события В равна P(B|Ai). Произведен опыт, в результате которого событие В наступило. Естественно после этого уточнить оценки вероятностей гипотез.
Апостериорные (от a posteriori (лат.) – на основе опыта) оценки
вероятностей гипотез Р(A1|B), Р(A2|B),…, Р(Ak|B) даются формулами Байеса. В
прикладной статистике существует направление «байесовская статистика», в
которой, в частности, на основе априорного распределения параметров после
проведения измерений, наблюдений, испытаний, опытов анализов вычисляют уточненные
оценки параметров.

