6.1. Модели стационарных и нестационарных временных
рядов, их идентификация
Пусть 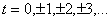 Рассмотрим
временной ряд X(t). Пусть сначала временной
ряд принимает числовые значения. Это могут быть, например, цены на батон хлеба
в соседнем магазине или курс обмена доллара на рубли в ближайшем обменном
пункте. Обычно в поведении временного ряда выявляют две основные тенденции -
тренд и периодические колебания.
Рассмотрим
временной ряд X(t). Пусть сначала временной
ряд принимает числовые значения. Это могут быть, например, цены на батон хлеба
в соседнем магазине или курс обмена доллара на рубли в ближайшем обменном
пункте. Обычно в поведении временного ряда выявляют две основные тенденции -
тренд и периодические колебания.
При этом под трендом понимают зависимость от времени
линейного, квадратичного или иного типа, которую выявляют тем или иным способом
сглаживания (например, экспоненциального сглаживания) либо расчетным путем, в
частности, с помощью метода наименьших квадратов. Другими словами, тренд - это
очищенная от случайностей основная тенденция временного ряда.
Временной ряд обычно колеблется вокруг тренда, причем
отклонения от тренда часто обнаруживают правильность. Часто это связано с
естественной или назначенной периодичностью, например, сезонной или недельной,
месячной или квартальной (например, в соответствии с графиками выплаты заплаты
и уплаты налогов). Иногда наличие периодичности и тем более ее причины неясны,
и задача эконометрика - выяснить, действительно ли имеется периодичность.
Элементарные методы оценки характеристик временных
рядов обычно достаточно подробно рассматриваются в курсах "Общей теории
статистики" (см., например, учебники [1,2]), поэтому нет необходимости
подробно разбирать их здесь. (Впрочем, о некоторых современных методах
оценивания длины периода и самой периодической составляющей речь пойдет ниже.)
Характеристики временных рядов. Для более подробного изучения временных рядов
используются вероятностно-статистические
модели. При этом временной ряд X(t) рассматривается
как случайный процесс (с дискретным временем) основными характеристиками
являются математическое ожидание X(t), т.е.
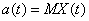 ,
,
дисперсия X(t), т.е.
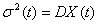
и автокорреляционная
функция временного ряда X(t)
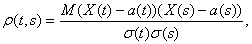
т.е.
функция двух переменных, равная коэффициенту корреляции между двумя значениями
временного ряда X(t) и X(s).
В теоретических и прикладных исследованиях
рассматривают широкий спектр моделей временных рядов. Выделим сначала стационарные модели. В них совместные функции распределения 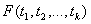 для любого числа моментов
времени k, а потому и все перечисленные выше
характеристики временного ряда не меняются со временем. В частности,
математическое ожидание и дисперсия являются постоянными величинами,
автокорреляционная функция зависит только от разности t-s. Временные ряды, не являющиеся стационарными, называются нестационарными.
для любого числа моментов
времени k, а потому и все перечисленные выше
характеристики временного ряда не меняются со временем. В частности,
математическое ожидание и дисперсия являются постоянными величинами,
автокорреляционная функция зависит только от разности t-s. Временные ряды, не являющиеся стационарными, называются нестационарными.
Линейные регрессионные модели с гомоскедастичными и гетероскедастичными, независимыми и автокоррелированными остатками. Как видно из сказанного выше, основное - это
"очистка" временного ряда от случайных отклонений, т.е. оценивание
математического ожидания. В отличие от простейших моделей регрессионного
анализа, рассмотренных в главе 5, здесь естественным образом появляются более
сложные модели. Например, дисперсия может зависеть от времени. Такие модели
называют гетероскедастичными, а те, в которых нет
зависимости от времени - гомоскедастичными. (Точнее
говоря, эти термины могут относиться не только к переменной "время",
но и к другим переменным.)
Далее, в главе 5 предполагалось, что погрешности
независимы между собой. В терминах настоящей главы это означало бы, что
автокорреляционная функция должна быть вырожденной - равняться 1 при равенстве
аргументов и 0 при их неравенстве. Ясно, что для реальных временных рядов так
бывает отнюдь не всегда. Если естественный ход изменений наблюдаемого процесса
является достаточно быстрым по сравнению с интервалом между последовательными
наблюдениями, то можно ожидать "затухания" автокорреляции" и
получения практически независимых остатков, в противном случае остатки будут автокоррелированы.
Идентификация моделей. Под идентификацией моделей обычно понимают выявление
их структуры и оценивание параметров. Поскольку структура - это тоже параметр,
хотя и нечисловой (см. главу 8), то речь идет об одной из типовых задач
эконометрики - оценивании параметров.
Проще всего задача оценивания решается для линейных
(по параметрам) моделей с гомоскедастичными независимыми остатками. Восстановление зависимостей во временных рядах может
быть проведено на основе методов наименьших квадратов и наименьших модулей,
рассмотренных в главе 5 моделей линейной (по параметрам) регрессии. На случай
временных рядов переносятся результаты, связанные с оцениванием необходимого
набора регрессоров, в частности, легко получить предельное геометрическое
распределение оценки степени тригонометрического полинома.
Однако на более общую ситуацию такого простого переноса сделать нельзя. Так, например, в случае
временного ряда с гетероскедастичными и автокоррелированными остатками снова можно воспользоваться
общим подходом метода наименьших квадратов, однако система уравнений метода
наименьших квадратов и, естественно, ее решение будут иными. Формулы в терминах
матричной алгебры, о которых упоминалось в главе 5, будут отличаться. Поэтому
рассматриваемый метод называется "обобщенный метод наименьших квадратов (ОМНК)" (см., например, [3, с.212]).
Замечание. Как
уже отмечалось в главе 5, простейшая модель метода наименьших квадратов
допускает весьма далекие обобщения, особенно в области системам одновременных
эконометрических уравнений для временных рядов. Для понимания соответствующей
теории и алгоритмов необходимо профессиональное владение матричной алгеброй.
Поэтому мы отсылаем тех, кому это интересно, к литературе по системам
эконометрических уравнений [4-9] и непосредственно по временным рядам [10-25], в которой особенно много интересуются спектральной теорией,
т.е. выделением сигнала из шума и разложением его на гармоники. Подчеркнем в
очередной раз, что за каждой главой настоящей книги стоит большая область
научных и прикладных исследований, вполне достойная того, чтобы посвятить ей
много усилий. Однако из-за ограниченности объема книги мы вынуждены изложение
сделать конспективным.

