Приложение 1
П-2. Центральные предельные теоремы
Простейший
вариант Центральной предельной теоремы (ЦПТ) теории вероятностей таков.
Центральная
предельная теорема (для одинаково распределенных слагаемых). Пусть X1, X2,…, Xn, …– независимые одинаково
распределенные случайные величины с математическими ожиданиями M(Xi) = m и дисперсиями D(Xi) =  , i = 1, 2,…, n,… Тогда для любого действительного
числа х существует предел
, i = 1, 2,…, n,… Тогда для любого действительного
числа х существует предел
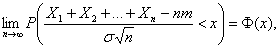
где Ф(х) – функция
стандартного нормального распределения.
Эту
теорему иногда называют теоремой Линдеберга-Леви [3, с.122].
В
ряде прикладных задач не выполнено условие одинаковой распределенности. В таких
случаях центральная предельная теорема обычно остается справедливой, однако на
последовательность случайных величин приходится накладывать те или иные
условия. Суть этих условий состоит в том, что ни одно слагаемое не должно быть
доминирующим, вклад каждого слагаемого в среднее арифметическое должен быть
пренебрежимо мал по сравнению с итоговой суммой. Наиболее часто используется
теорема Ляпунова.
Центральная
предельная теорема (для разнораспределенных слагаемых) – теорема
Ляпунова. Пусть X1, X2,…, Xn, …– независимые случайные величины с математическими
ожиданиями M(Xi) = mi и дисперсиями D(Xi) = 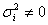 , i = 1, 2,…, n,… Пусть при некотором δ>0 у
всех рассматриваемых случайных величин существуют центральные моменты порядка
2+δ и безгранично убывает «дробь Ляпунова»:
, i = 1, 2,…, n,… Пусть при некотором δ>0 у
всех рассматриваемых случайных величин существуют центральные моменты порядка
2+δ и безгранично убывает «дробь Ляпунова»:

где
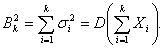
Тогда для любого действительного
числа х существует предел
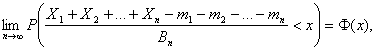 (1)
(1)
где Ф(х) – функция стандартного
нормального распределения.
В
случае одинаково распределенных случайных слагаемых
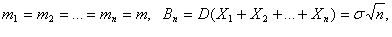
и теорема Ляпунова переходит в
теорему Линдеберга-Леви.
История
получения центральных предельных теорем для случайных величин растянулась на
два века – от первых работ Муавра в 30-х годах 18-го века для необходимых и
достаточных условий, полученных Линдебергом и Феллером в 30-х годах 20-го века.
Теорема
Линдеберга-Феллера. Пусть X1, X2,…, Xn, …, – независимые случайные величины
с математическими ожиданиями M(Xi) = mi и дисперсиями D(Xi) = 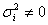 , i = 1, 2,…, n,… Предельное соотношение (1), т.е.
центральная предельная теорема, выполнено тогда и только тогда, когда при любом
τ>0
, i = 1, 2,…, n,… Предельное соотношение (1), т.е.
центральная предельная теорема, выполнено тогда и только тогда, когда при любом
τ>0
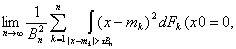
где Fk(x) обозначает функцию распределения
случайной величины Xk.
Доказательства
перечисленных вариантов центральной предельной теоремы для случайных величин
можно найти в классическом курсе теории вероятностей [2].
Для
прикладной статистики и, в частности, для нечисловой статистики большое
значение имеет многомерная центральная предельная теорема. В ней речь идет не о
сумме случайных величин, а о сумме случайных векторов.
Необходимое и достаточное условие многомерной
сходимости [3, с.124]. Пусть Fn обозначает совместную функцию
распределения k-мерного случайного вектора 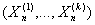 , n = 1,2,…, и Fλn – функция распределения линейной
комбинации
, n = 1,2,…, и Fλn – функция распределения линейной
комбинации 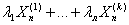 . Необходимое и достаточное условие для сходимости Fn к некоторой k-мерной функции распределения F состоит в том, что Fλn имеет предел для любого вектора
λ.
. Необходимое и достаточное условие для сходимости Fn к некоторой k-мерной функции распределения F состоит в том, что Fλn имеет предел для любого вектора
λ.
Приведенная
теорема ценна тем, что сходимость векторов сводит к сходимости линейных
комбинаций их координат, т.е. к сходимости обычных случайных величин,
рассмотренных ранее. Однако она не дает возможности непосредственно указать
предельное распределение. Это можно сделать с помощью следующей теоремы.
Теорема
о многомерной сходимости. Пусть Fn и Fλn – те же, что в предыдущей теореме.
Пусть F - совместная функция распределения k-мерного случайного вектора 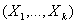 . Если функция распределения Fλn сходится при росте объема выборки к
функции распределения Fλ для любого вектора λ, где Fλ – функция распределения линейной
комбинации
. Если функция распределения Fλn сходится при росте объема выборки к
функции распределения Fλ для любого вектора λ, где Fλ – функция распределения линейной
комбинации 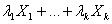 , то Fn сходится к F.
, то Fn сходится к F.
Здесь
сходимость Fn к F означает, что для любого k-мерного вектора 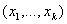 такого, что функция
распределения F непрерывна в
такого, что функция
распределения F непрерывна в 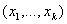 , числовая последовательность Fn
, числовая последовательность Fn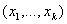 сходится при росте n к числу F
сходится при росте n к числу F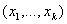 . Другими словами, сходимость функций распределения
понимается ровно также, как при обсуждении предельных теорем для случайных величин выше. Приведем многомерный
аналог этих теорем.
. Другими словами, сходимость функций распределения
понимается ровно также, как при обсуждении предельных теорем для случайных величин выше. Приведем многомерный
аналог этих теорем.
Многомерная
центральная предельная теорема [3]. Рассмотрим независимые одинаково
распределенные k-мерные случайные вектора
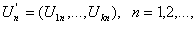
где штрих обозначает операцию транспонирования
вектора. Предположим, что случайные вектора Un имеют моменты первого и второго
порядка, т.е.
М(Un) = μ, D(Un) = Σ,
где μ – вектор математических ожиданий
координат случайного вектора, Σ – его ковариационная матрица. Введем последовательность
средних арифметических случайных векторов:
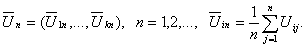
Тогда случайный вектор 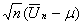 имеет асимптотическое k-мерное нормальное распределение
имеет асимптотическое k-мерное нормальное распределение 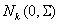 , т.е. он асимптотически распределен так же, как k-мерная нормальная величина с нулевым
математическим ожиданием, ковариационной Σ и плотностью
, т.е. он асимптотически распределен так же, как k-мерная нормальная величина с нулевым
математическим ожиданием, ковариационной Σ и плотностью
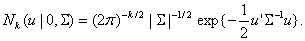
Здесь |Σ| - определитель матрицы Σ.
Другими словами, распределение случайного вектора 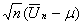 сходится к k-мерному нормальному распределению с
нулевым математическим ожиданием и ковариационной матрицей Σ.
сходится к k-мерному нормальному распределению с
нулевым математическим ожиданием и ковариационной матрицей Σ.
Напомним,
что многомерным нормальным распределением с математическим ожиданием μ и
ковариационной матрицей Σ называется распределение, имеющее плотность

Многомерная
центральная предельная теорема показывает, что распределения сумм независимых
одинаково распределенных случайных векторов при большом числе слагаемых хорошо
приближаются с помощью нормальных распределений, имеющих такие же первые два
момента (вектор математических ожиданий координат случайного вектора и его
корреляционную матрицу), как и исходные вектора. От одинаковой распределенности
можно отказаться, но это потребует некоторого усложнения символики. В целом из
теоремы о многомерной сходимости вытекает, что многомерный случай ничем
принципиально не отличается от одномерного.
Пример. Пусть X1,
… Xn ,…– независимые одинаково
распределенные случайные величины. Рассмотрим k-мерные независимые одинаково
распределенные случайные вектора
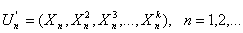
Их математическое ожидание – вектор
теоретических начальных моментов, а ковариационная матрица составлена из
соответствующих центральных моментов. Тогда  - вектор выборочных центральных моментов. Многомерная
центральная предельная теорема утверждает, что
- вектор выборочных центральных моментов. Многомерная
центральная предельная теорема утверждает, что  имеет асимптотически
нормальное распределение. Как вытекает из теорем о наследовании сходимости и о
линеаризации (см. ниже), из распределения
имеет асимптотически
нормальное распределение. Как вытекает из теорем о наследовании сходимости и о
линеаризации (см. ниже), из распределения  можно вывести
распределения различных функций от выборочных начальных моментов. А поскольку
центральные моменты выражаются через начальные моменты, то аналогичное
утверждение верно и для них.
можно вывести
распределения различных функций от выборочных начальных моментов. А поскольку
центральные моменты выражаются через начальные моменты, то аналогичное
утверждение верно и для них.

