Глава 2. Статистические методы в
пространствах произвольной природы
2.3. Экстремальные статистические задачи
Если
проанализировать приведенные выше в разделах 2.1 и 2.2 постановки и результаты,
касающиеся эмпирических и теоретических средних и законов больших чисел, то
становится очевидной возможность их обобщения. Так, доказательства теорем
практически не меняются, если считать, что функция f(x,y)
определена на декартовом произведении бикомпактных пространств X и Y,
а не на X2. Тогда можно считать, что элементы выборки лежат в Х, а Y - пространство параметров, подлежащих оценке.
Обобщения
законов больших чисел. Пусть, например, выборка х1 = х1(ω), х2 = х2(ω),
… , хn = хn(ω) взята из распределения с
плотностью p(x,y), где у – неизвестный параметр. Если положить
f(x,y) = - ln p(x,y),
то задача нахождения эмпирического
среднего
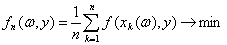
переходит в задачу оценивания
неизвестного параметра y методом максимального правдоподобия
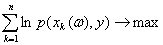 .
.
Соответственно законы больших чисел
переходят в утверждения о состоятельности этих оценок в случае пространств X и Y общего вида. При такой
интерпретации функция f(x,y) уже не является расстоянием или
показателем различия. Однако для доказательства сходимости оценок к
соответствующим значениям параметров это и не требуется. Достаточно
непрерывности этой функции на декартовом произведении бикомпактных пространств X и Y.
В
случае функции f(x,y) общего вида можно говорить об определении в
пространствах произвольной природы аналогов оценок минимального контраста,
достаточно хорошо изученных в классической математической статистике, и о
состоятельности таких оценок. Пусть при каждом конкретном значении параметра у справедливо предельное соотношение

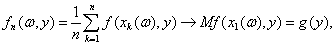
где f – функция контраста. Тогда состоятельность
оценок минимального контраста вытекает из справедливости предельного перехода
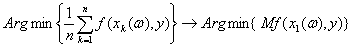 .
.
Частными случаями оценок минимального
контраста являются, устойчивые (робастные) оценки Тьюки-Хубера [1, 6-9], а
также оценки параметров в задачах аппроксимации (параметрической регрессии) в
пространствах произвольной природы (см. ниже раздел 2.7).
Можно
пойти и дальше в обобщении законов больших чисел. Пусть известно, что при
каждом конкретном y при безграничном росте n имеет быть
сходимость по вероятности
fn(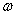 , y)
, y) 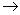 f(y),
f(y),
где fn(ω, y) –
последовательность случайных функций на пространстве Y, а f(y)
– некоторая функция на У. В каких случаях и в каком смысле имеет место
сходимость
Argmin {fn(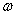 , y), y
, y), y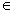 X}
X} 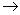 Argmin {f(y),
y
Argmin {f(y),
y 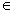 X}?
X}?
Другими словами, когда из поточечной
сходимости функций вытекает сходимость точек минимума?
Причем
здесь можно под n понимать натуральное число. А можно рассматривать
сходимость по направленному множеству (см. приложение 1), или же, что
практически то же самое – «сходимость по фильтру» в смысле Картана и Бурбаки
[3, с.118]. В частности, можно описывать ситуацию вектором, координаты которого
- объемы нескольких выборок, и все они безгранично растут. В классической
математической статистике такие постановки рассматривать не любят, поскольку
без использования понятия направленного множества трудно строго описать
подобный предельный переход.
Поскольку,
как хорошо известно, основные задачи прикладной статистики можно представить в
виде оптимизационных задач, то ответ на поставленный вопрос о сходимости точек
минимума дает возможность единообразного подхода к изучению асимптотики решений
разнообразных экстремальных статистических задач. Одна из возможных
формулировок, основанная на бикомпактности пространств Х и У и
нацеленная на изучение оценок минимального контраста, дана и обоснована выше.
Другой подход развит в работе [4]. Он основан на использовании понятий
асимптотической равномерной разбиваемости и координатной асимптотической
равномерной разбиваемости пространств. С помощью указанных подходов удается
стандартным образом обосновывать состоятельность оценок характеристик и
параметров в основных задачах прикладной статистики.
Рассматриваемую
тематику можно развивать дальше, в частности, рассматривать аналоги законов
больших чисел в случае пространств, не являющихся бикомпактными, а также
изучать скорость сходимости Argmin{fn(x(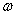 ), y), y
), y), y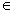 X} к Argmin{f(y), y
X} к Argmin{f(y), y 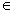 X}.
X}.
Примеры
применения результатов о предельном поведении точек минимума приведены ниже. В
частности, экстремальный вид имеют параметрические задачи восстановления зависимостей,
в том числе задачи оценивание информативных подмножеств признаков (раздел 2.7).
Ряд методов классификации основан на решении оптимизационных задач, в
частности, так ищут оптимальное разбиение пространства и «центры» кластеров
(раздел 2.8). При снижении размерности пространства с целью сжатия информации,
в частности, методами главных компонент, метрического и неметрического
многомерного шкалирования необходимо решать экстремальные статистические задачи
рассмотренного выше вида (раздел 2.9).

