Частоты

Из приведенного выше определения математической статистики следует, что описание статистических данных дается с помощью частот. Частота – это отношение числа Х наблюдаемых единиц, которые принимают заданное значение или лежат в заданном интервале, к общему числу наблюдений n, т.е. частота – это Х/n. (В более старой литературе иногда Х/n называется относительной частотой, а под частотой имеется в виду Х. В старой терминологии можно сказать, что относительная частота – это отношение частоты к общему числу наблюдений.)

Отметим, что обсуждаемое определение приспособлено к нуждам одномерной статистики. В случае многомерного статистического анализа, статистики случайных процессов и временных рядов, статистики объектов нечисловой природы нужны несколько иные определения понятия «статистические данные». Не считая нужным давать такие определения, отметим, что в подавляющем большинстве практических постановок исходные статистические данные – это выборка или несколько выборок. А выборка – это конечная совокупность соответствующих математических объектов (чисел, векторов, функций, объектов нечисловой природы).

Число Х имеет биномиальное распределение, задаваемое вероятностью р того, что случайная величина, с помощью которой моделируются результаты наблюдений, принимает заданное значение или лежит в заданном интервале, и общим числом наблюдений n. Из закона больших чисел (теорема Бернулли) следует, что

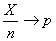
при n→∞ (сходимость по вероятности), т.е. частота сходится к вероятности. Теорема Муавра-Лапласа позволяет уточнить скорость сходимости в этом предельном соотношении.