Параметрические и непараметрические гипотезы

Статистические гипотезы бывают параметрические и непараметрические. Предположение, которое касается неизвестного значения параметра распределения, входящего в некоторое параметрическое семейство распределений, называется параметрической гипотезой (напомним, что параметр может быть и многомерным). Предположение, при котором вид распределения неизвестен (т.е. не предполагается, что оно входит в некоторое параметрическое семейство распределений), называется непараметрической гипотезой. Таким образом, если распределение F(x) результатов наблюдений в выборке согласно принятой вероятностной модели входит в некоторое параметрическое семейство {F(x;θ), θ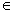Θ}, т.е. F(x) = F(x;θ₀) при некотором θ₀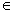Θ, то рассматриваемая гипотеза – параметрическая, в противном случае – непараметрическая.

Если и Н₀ и Н₁ – параметрические гипотезы, то задача проверки статистической гипотезы – параметрическая. Если хотя бы одна из гипотез Н₀ и Н₁ – непараметрическая, то задача проверки статистической гипотезы – непараметрическая. Другими словами, если вероятностная модель ситуации – параметрическая, т.е. полностью описывается в терминах того или иного параметрического семейства распределений вероятностей, то и задача проверки статистической гипотезы – параметрическая. Если же вероятностная модель ситуации – непараметрическая, т.е. ее нельзя полностью описать в терминах какого-либо параметрического семейства распределений вероятностей, то и задача проверки статистической гипотезы – непараметрическая. В примерах 11-13, 16, 17, 20-22 даны постановки параметрических задач проверки гипотез, а в примерах 14, 15, 18, 19, 23-25 – непараметрических. Непараметрические задачи делятся на два класса: в одном из них речь идет о проверке утверждений, касающихся функций распределения (примеры 14, 15, 18, 19, 25), во втором – о проверке утверждений, касающихся характеристик распределений (примеры 23, 24).

Статистическая гипотеза называется простой, если она однозначно задает распределение результатов наблюдений, вошедших в выборку. В противном случае статистическая гипотеза называется сложной. Гипотеза 2 из приведенного выше списка, нулевые гипотезы в примерах 11, 12, 14, 20, нулевая и альтернативная гипотезы в примере 21 – простые, все остальные упомянутые выше гипотезы – сложные.