Распределение
Пуассона
Третье широко используемое дискретное распределение –
распределение Пуассона. Случайная величина Y имеет распределение Пуассона, если
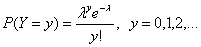 ,
,
где λ – параметр распределения
Пуассона, и P(Y=y)=0 для всех прочих y (при y=0 обозначено 0! =1). Для
распределения Пуассона
M(Y) = λ, D(Y) = λ.
Это распределение названо в честь
французского математика С.Д.Пуассона (1781-1840), впервые получившего его в
1837 г. Распределение Пуассона является предельным случаем биномиального
распределения, когда вероятность р осуществления события мала, но число
испытаний n велико, причем np = λ. Точнее, справедливо предельное соотношение
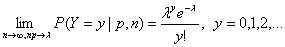
Поэтому распределение Пуассона (в
старой терминологии «закон распределения») часто называют также «законом редких
событий».
Распределение
Пуассона возникает в теории потоков событий (см. выше). Доказано, что для
простейшего потока с постоянной интенсивностью Λ число событий (вызовов),
происшедших за время t, имеет распределение Пуассона с параметром λ =
Λt. Следовательно, вероятность того, что за время t не произойдет ни одного события,
равна e-Λt, т.е. функция распределения длины
промежутка между событиями является экспоненциальной.
Распределение
Пуассона используется при анализе результатов выборочных маркетинговых обследований
потребителей, расчете оперативных характеристик планов статистического
приемочного контроля в случае малых значений приемочного уровня дефектности,
для описания числа разладок статистически управляемого технологического
процесса в единицу времени, числа «требований на обслуживание», поступающих в
единицу времени в систему массового обслуживания, статистических
закономерностей несчастных случаев и редких заболеваний, и т.д.
Описание
иных параметрических семейств дискретных распределений и возможности их
практического использования рассматриваются в обширной (более миллиона названий
статей и книг на десятках языков) литературе по вероятностно-статистическим
методам.

