Независимость
случайных величин
Независимость
случайных величин –
одно из базовых понятий теории вероятностей, лежащее в основе практических всех
вероятностно-статистических методов принятия решений.
Определение
4. Случайные величины Х и У, определенные на одном и том же
пространстве элементарных событий, называются независимыми, если для любых
чисел а и b независимы события {X=a} и {Y=b}.
Утверждение 6. Если случайные величины Х и У независимы, а и b – некоторые числа, то случайные величины X+a и Y+b также независимы.
Действительно, события {X+a=с} и {Y+b=d} совпадают с событиями {X=с-a} и {Y=d-b} соответственно, а потому
независимы.
Пример
7. Случайные величины, определенные по результатам различных испытаний в
схеме независимых испытаний, сами независимы. Это вытекает из того, что
события, с помощью которых определяется независимость случайных величин,
определяются по результатам различных испытаний, а потому независимы по
определению независимых испытаний.
В
вероятностно-статистических методах принятия решений постоянно используется
следующий факт: если Х и У – независимые случайные величины, f(X) и g(Y) – случайные величины, полученные из Х и У с помощью некоторых функций f и g, то f(X) и g(Y) – также независимые случайные величины. Например,
если Х и У независимы, то Х2 и 2У+3
независимы, logX и logУ независимы. Доказательство рассматриваемого факта – тема одной из
контрольных задач в конце главы.
Подавляющее
большинство вероятностно-статистических моделей, используемых на практике,
основывается на понятии независимых случайных величин. Так, результаты
наблюдений, измерений, испытаний, анализов, опытов обычно моделируются
независимыми случайными величинами. Часто считают, что наблюдения проводятся
согласно схеме независимых испытаний. Например, результаты
финансово-хозяйственной деятельности предприятий, выработка рабочих, результаты
(данные) измерений контролируемого параметра у изделий, отобранных в выборку
при статистическом регулировании технологического процесса, ответы потребителей
при маркетинговом опросе и другие типы данных, используемых при принятии
решений, обычно рассматриваются как независимые случайные величины, вектора или
элементы. Причина такой популярности понятия независимости случайных величин
состоит в том, что к настоящему времени теория продвинута существенно дальше
для независимых случайных величин, чем для зависимых.
Часто используется следующее свойство
независимых случайных величин.
Утверждение
7. Если случайные величины Х и У независимы, то
математическое ожидание произведения ХУ равно произведению математических
ожиданий Х и У, т.е. М(ХУ)=М(Х)М(У).
Доказательство. Пусть Х принимает
значения х1, х2,…, хm, в то время как У принимает
значения у1, у2,…, уk. Сгруппируем в задающей М(ХУ) сумме члены, в
которых Х и У принимают фиксированные значения:
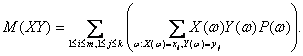 (6)
(6)
Поскольку постоянный множитель можно
вынести за знак суммы, то
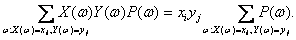
Из последнего равенства и определения
вероятности события заключаем, что равенство (6) можно преобразовать к виду
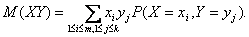
Так как Х и У независимы, то 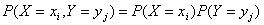 .
Воспользовавшись этим равенством и свойством символа суммирования
.
Воспользовавшись этим равенством и свойством символа суммирования
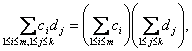
заключаем, что
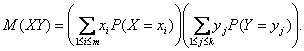 (7)
(7)
Из равенства (5) следует, что первый
сомножитель в правой части (7) есть М(Х), а второй – М(У), что и
требовалось доказать.
Пример
8. Построим пример, показывающий, что из равенства М(ХУ)=М(Х)М(У) не
следует независимость случайных величин Х и У. Пусть
вероятностное пространство состоит из трех равновероятных элементов 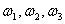 . Пусть
. Пусть
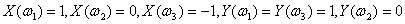 .
.
Тогда ХУ = Х, М(Х) = М(ХУ) =
0, следовательно, М(ХУ) = М(Х)М(У). Однако при этом Р(Х=0) =
Р(У=0) = Р(Х=0, У=0) = 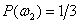 , в то
время как вероятность события {X=0, Y=0} в случае независимых Х и У должна
была равняться
, в то
время как вероятность события {X=0, Y=0} в случае независимых Х и У должна
была равняться 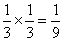 .
.
Независимость нескольких случайных величин X, Y, Z,… означает по определению, что для
любых чисел x, y, z,… справедливо равенство
P(X=x, Y=y, Z=z,…) = P(X=x) P(Y=y) P(Z=z)…
Например, если случайные
величины определяются по результатам различных испытаний в схеме независимых испытаний,
то они независимы.

