Часть 3. Методы прикладной статистики

3.4. Статистика нечисловых данных

3.4.2. Теория случайных толерантностей

          В прикладных исследованиях обычно используют три конкретных вида бинарных отношений – ранжировки, разбиения и толерантности. Статистические теории ранжировок [13] и разбиений [15] достаточно сложны с математиче6ской точки зрения. Поэтому продвинуться удается не очень далеко. Теория случайных ранжировок, в частности, изучает в основном равномерные распределения на множестве ранжировок. Теория случайных толерантностей позволяет рассмотреть более общие ситуации. Это объясняется, грубо говоря, тем, что для теории толерантностей оказываются полезными суммы некоторых независимых случайных величин, а для теории ранжировок и разбиений аналогичные случайные величины зависимы. Теория случайных толерантностей является частным случаем теории люсианов, рассматриваемой в подразделе 3.4.3. Здесь приводим результаты, специфичные именно для толерантностей.

          Пусть X - конечное множество из k элементов. Толерантность А на множестве Х, как и любое бинарное отношение, однозначно описывается матрицей ||a(i, j)||, 1 < i, j < k, где a(i, j) = 1, если элементы с номерами i и j связаны отношением толерантности, и a(i, j) = 0 в противном случае. Поскольку толерантность – это рефлексивное и симметричное бинарное отношение, то достаточно рассматривать часть матрицы, лежащую над главной диагональю: ||a(i, j), 1 < i<j < k||. Между наборами ||a(i, j), 1 < i<j < k|| из 0 и 1 и толерантностями на Х имеется взаимнооднозначное соответствие.

          Пусть А = А(ω) – случайная толерантность, равномерно распределенная на множестве всех толерантностей на Х. Легко видеть, что в этом случае a(i, j), 1 < i<j < k, - независимые случайные величины, принимающие значения 0 и 1 с вероятностями 0,5. Этот факт, несмотря на свою математическую тривиальность, является решающим для построения теории толерантностей. Для аналогичных постановок в теории ранжировок и разбиений величины a(i, j) оказываются зависимыми.

          Следовательно, случайная величина

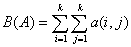
имеет биномиальное распределение с параметрами k(k-1)/2, ½ и асимптотически нормальна при k → ∞.

          Проверка гипотез о согласованности. Рассмотрим s независимых толерантностей А₁, А₂, …, А_s, равномерно распределенных на множестве всех толерантностей на Х. Рассмотрим вектор

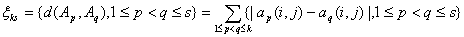,  (1)

где d(A_p, A_q) – расстояние между толерантностями A_p и A_q, аксиоматически введенное в главе 1.1. В (1) предполагается, что пары (p, q), p < q, располагаются в раз навсегда установленном порядке, для определенности в лексиграфическом (т.е. пары упорядочиваются в соответствии со значением р, а при одинаковых р – по значению q).

          Вектор ξ_ks является суммой k(k-1)/2 независимых одинаково распределенных случайных векторов, а потому асимптотически нормален при k → ∞. Координаты этого вектора независимы, поскольку, как нетрудно видеть, координаты каждого слагаемого независимы (это свойство не сохраняется при отклонении от равномерности распределения). Распределения случайных величин a_p(i, j) и |a_p(i, j) - a_q(i, j)| совпадают, поэтому распределения В(А) и d(A_p, A_q) также совпадают.

          В силу многомерной центральной предельной теоремы (глава 1.4) распределение вектора

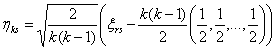
сходится при k → ∞ к распределению многомерного нормального вектора η_s, ковариационная матрица которого совпадает с ковариационной матрицей вектора η_ks, а математическое ожидание равно 0. Таким образом, координаты случайного вектора η_s независимы и имеют стандартное нормальное распределение с математическим ожиданием 0 и дисперсией 1. В соответствии с теоремами о наследовании сходимости (глава 1.4) распределение f(η_ks) сходится при k → ∞ к распределению f(η_s) для достаточно широкого класса функций f, в частности, для всех непрерывных функций. В качестве примеров рассмотрим статистики

.

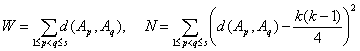При k → ∞ распределения случайных величин

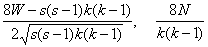
сходятся соответственно к стандартному нормальному распределению с математическим ожиданием 0 и дисперсией 1 и распределению хи-квадрат с s(s – 1)/2 степенями свободы. Статистики W и N могут быть использованы для проверки гипотезы о равномерности распределения толерантностей.

          Как известно, в теории ранговой корреляции [13], т.е. в теории случайных ранжировок, в качестве единой выборочной меры связи нескольких признаков используется коэффициент согласованности W(R), называемый также коэффициентом конкордации [16, табл.6.10]. Его распределение затабулировано в предположении равномерности распределения на пространстве ранжировок (без связей). Непосредственным аналогом W(R) в случае толерантностей является статистика W. Статистики W и N играют ту же роль для толерантностей, что W(R) для ранжировок, однако математико-статистическая теория в случае толерантностей гораздо проще, чем для ранжировок.

          Обобщением равномерно распределенных толерантностей являются толерантности с независимыми связями. В этой постановке предполагается, что  a(i, j), 1 < i<j < k, - независимые случайные величины, принимающие значения 0 и 1. Обозначим Р(a(i, j) = 1) = р(i,j). Тогда Р(a(i, j) = 0) = 1 - р(i,j). Таким образом, распределение толерантности с независимыми связями задается нечеткой толерантностью, т.е. вектором

P = {р(i, j), 1 < i<j < k}.

          Пусть имеется s независимых случайных толерантностей А₁, А₂, …, А_s с независимыми связями, распределения которых задаются векторами Р₁, Р₂, …, Р_s соответственно. Рассмотрим проверку гипотезы согласованности

Н₀: Р₁ = Р₂ =…= Р_s.

Она является более слабой, чем гипотеза равномерности

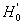: Р₁ = Р₂ =…= Р_s =(½, ½, ..., ½),

для проверки которой используют статистики W и N (см. выше).

          Пусть сначала s = 2. Тогда

P{|a₁(i, j) - a₂(i, j)| = 1} = q(i, j), P{|a₁(i, j) - a₂(i, j)| = 0} = 1 - q(i, j),

где

q(i, j) = p₁(i, j) (1 - p₂(i, j)) + p₂(i, j) (1 - p₁(i, j)).

Следовательно, расстояние d(A₁, A₂) между двумя случайными толерантностями с независимыми связями есть сумма k(k - 1)/2 независимых случайных величин, принимающих значения 0 и 1, причем математическое ожидание и дисперсия d(A₁, A₂) таковы:

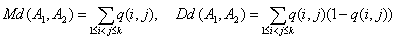.      (2)

          Пусть k → ∞. Если Dd(A₁, A₂) → ∞, то условие Линденберга Центральной Предельной Теоремы теории вероятностей выполнено (см. главу 1.4), и распределение нормированного расстояния

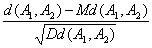        (3)

сходится к стандартному нормальному распределению с математическим ожиданием 0 и дисперсией 1. Если существует число δ > 0 такое, что при всех k, i, j, 1 < i<j < k, вероятности p₁(i, j) и p₂(i, j) лежат внутри интервала (δ; 1 – δ), то Dd(A₁, A₂) → ∞.

          Соотношения (2), (3) и им подобные позволяют рассчитать мощность критериев, основанных на статистиках W и N, при k → ∞, подобно тому, как это сделано в [1, глава 4.5]. Поскольку подобные расчеты не требуют новых идей, не будем приводить их здесь.

          Обычно Р₁ и Р₂ неизвестны. Для проверки гипотезы Р₁ = Р₂ в некоторых случаях можно порекомендовать отвергать гипотезу на уровне значимости α, если d(A₁, A₂) > d₀, где d₀ есть (1-α)-квантиль распределения расстояния между двумя независимыми равномерно распределенными случайными толерантностями, т.е. квантиль биномиального распределения В(А). Укажем достаточные условия такой рекомендации.

          Пусть

р =(p₁(i, j) + p₂(i, j))/2,   p₁(i, j) = р + Δ,

тогда

p₂(i, j) = р – Δ,   q= q(i, j) = 2р(1 – р) + 2Δ².                  (4)

Если существует число δ > 0 такое, что

q – ½ > δ > 0                 (5)

при всех k, i, j, то гипотеза Р₁ = Р₂ будет отвергаться с вероятностью, стремящейся к 1 при k → ∞. Из (4) следует, что при фиксированном р существует Δ такое, что выполнено (5), тогда и только тогда, когда 0,25 < p < 0,75.

          Своеобразие постановки задачи проверки гипотезы состоит в том, что при росте k число неизвестных параметров, т.е. координат векторов P_i, растет пропорционально объему данных. Поэтому и столь далекая от оптимальности процедура, как описанная в двух предыдущих абзацах, представляет некоторый практический интерес. Для случая s > 4 в теории люсианов (глава 3.4.3) разработаны методы проверки гипотезы согласованности Н₀: Р₁ = Р₂ =…= Р_s.

          Нахождение группового мнения. Пусть А₁, А₂, …, А_s - случайные толерантности, описывающие мнения s экспертов. Для нахождения группового мнения будем использовать медиану Кемени, т.е. эмпирическое среднее относительно расстояния, введенного в главе 1.1. Медианой Кемени является

.

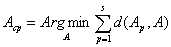Легко видеть, что А_ср = ||a_ср(i, j)|| удовлетворяет условию: a_ср(i, j) = 1, если

,

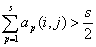и a_ср(i, j) = 0, если

.

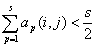Следовательно, при нечетном s групповое мнение А_ср определяется однозначно. При четном s неоднозначность возникает в случае

.

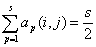Тогда медиана Кемени А_ср - не одна толерантность, а множество толерантностей, минимум суммы расстояний достигается и при a_ср(i,j) = 1, и при a_ср(i, j) = 0.

          Асимптотическое поведение группового мнения (медианы Кемени для толерантностей) вытекает из общих результатов о законах больших чисел в пространствах произвольной природы (глава 2.1), поэтому рассматривать его здесь нет необходимости.

          Дихотомические (бинарные) признаки в классической асимптотике. Многое в предыдущем изложении определялось спецификой толерантностей. В частности, особая роль равномерности распределения на множестве всех толерантностей оправдывала специальное рассмотрение статистик W и N; аксиоматически введенное расстояние d между толерантностями играло важную роль в приведенных выше результатах. Однако модель толерантностей с независимыми связями уже меньше связана со спецификой толерантностей. В ней толерантности можно рассматривать просто как частный случай люсианов. Широко применяется следующая модель порождения данных.

          Пусть А₁, А₂, …, А_s - независимые люсианы. Это значит, что статистические данные имеют вид

(А₁, А₂, …, А_s) = ||X_ij, i = 1,2, ..., s; j = 1, 2, ..., k||,           (6)

где X_ij - независимые в совокупности испытания Бернулли с вероятностями успеха

(Р₁, Р₂, …, Р_s) = ||p_ij, , i = 1,2, ..., s; j = 1, 2, ..., k||,                   (7)

где P_i - вектор вероятностей, описывающий распределение люсиана A_i. Особое значение имеют одинаково распределенные люсианы, для которых Р₁ = Р₂ =…= Р_s = Р, где символом Р обозначен общий вектор вероятностей.

          Как обычно в математической статистике, содержательные результаты при изучении модели (6) - (7) можно получить в асимптотических постановках. При этом есть два принципиально разных предельных перехода: s → ∞ и k → ∞. Первый из них - традиционный: число неизвестных параметров постоянно, объем выборки s растет. Во втором число параметров растет, объем выборки остается постоянным, но общий объем данных ks растет пропорционально числу неизвестных параметров. Аналогом является асимптотическое изучение коэффициентов ранговой корреляции Кендалла и Спирмена: число ранжировок, т.е. объем выборки, постоянно (и равно 2), а число ранжируемых объектов растет.

          Вторая постановка изучается в следующем подразделе, посвященном люсианам. Некоторые задачи в первой постановке рассмотрим здесь.

          Случайные толерантности используются, в частности, для оценки нечетких толерантностей [1]. Для описания результатов опроса группы экспертов о сходстве объектов строят нечеткую толерантность M = ||μ_ij||, μ_ij = l_ij/n_ij, где n_ij - число ответов о сходстве i-го и j-го объектов, а l_ij - число положительных ответов из них. Если эксперты действуют в соответствии с единым вектором параметров Р, то М - состоятельная оценка для Р. Следующий вопрос при таком подходе - верно ли, что две группы экспертов «думают одинаково», т.е. используют совпадающие вектора Р? Рассмотрим эту постановку на более общем языке люсианов.

          Пусть A₁, A₂, ..., A_m и B₁, B₂, ..., B_n - независимые в совокупности люсианы, одинаково распределенные в каждой группе с параметрами Р(А) и Р(В) соответственно. Требуется проверить гипотезу Р(А) = Р(В). Естественным является переход к пределу при min(m, n) → ∞.

          Пусть гипотеза справедлива. Предположим, что p_i = p_i(A) = p_i(B) ≠ 0 при всех i = 1, 2, ..., k. (Разбор нарушений этого условия очевиден.) Пусть s_i - число единиц на i-м месте в первой группе люсианов, а t_i - во второй. Рассмотрим случайные величины

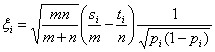.              (8)

Они независимы в совокупности. В соответствии с результатами главы 1.4 распределения ξ_i при min(m, n) → ∞ сходятся к стандартному нормальному распределению с математическим ожиданием 0 и дисперсией 1. Эти свойства сохраняются при замене p_i в (8) на состоятельные оценки, построенные по статистическим данным, соответствующим i-му месту. Будем использовать эффективную оценку [17, с.52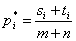9]

.          (9)

Подставим (9) в (8), получим статистики

.

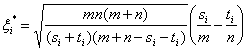Полученные статистики можно использовать для проверки рассматриваемой гипотезы, например, с помощью критериев, основанных на статистиках

.

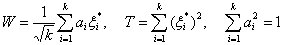С помощью результатов главы 1.4 получаем, что W имеет в пределе при min(m, n) → ∞ стандартное нормальное распределение, а Т - распределение хи-квадрат с k степенями свободы.

          Рассмотрим распределение статистики W при альтернативных гипотезах. Положим

.

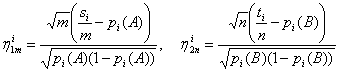Эти случайные величины независимы, распределение каждой из них при min(m, n) → ∞ сходится к стандартному нормальному распределению. Поскольку

,

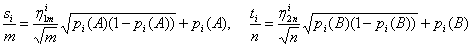то

,

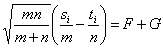где

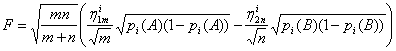
и

.

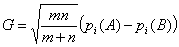В силу результатов главы 1.4 распределение F при min(m, n) → ∞ сближается с нормальным распределением, математическое ожидание которого равно 0, а дисперсия

.

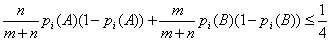Поэтому, чтобы получить собственное (т.е. невырожденное) распределение W при альтернативах, естественно рассмотреть модель

,

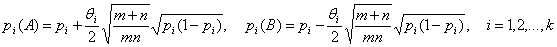где θ_i - некоторые фиксированные числа. Тогда при min(m, n) → ∞ оценки 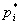 из (9) сходятся к p_i и  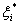являются независимыми асимптотически нормальными случайными величинами с математическими ожиданиями θ_i и единичными дисперсиями. Опираясь на результаты главы 1.4, заключаем, что распределение статистики W сходится к нормальному распределению с математическим ожиданием

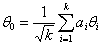
и единичной дисперсией.

          Если в последней формуле θ₀ = 0, то асимптотическое распределение W таково же, как и в случае справедливости нулевой гипотезы. От указанного недостатка свободна статистика Т. Тем же путем, как и для W, получаем, что при min(m, n) → ∞ распределение Т сходится к нецентральному хи-квадрат распределению с k степенями свободы и параметром нецентральности

.

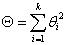          Можно рассматривать ряд других задач, например, проверку совпадения параметров для нескольких групп люсианов (аналог дисперсионного анализа), установление зависимости Р(В) от Р(А) (аналог регрессионного анализа), отнесение вновь поступающего люсиана к одной из групп (задача диагностики - аналог дискриминантного анализа; представляет интерес, например, при применении тестов типа MMPI оценки психического состояния личности) и т.д. Однако принципиальных трудностей на пути развития соответствующих методов не видно, и мы не будем их здесь рассматривать. Создание соответствующих алгоритмов проводится специалистами по прикладной статистике в соответствии с непосредственными заказами пользователей.