Непараметрическое
оценивание математического ожидания
В непараметрической постановке оценивают либо характеристики
случайной величины (математическое ожидание, дисперсию, коэффициент вариации),
либо ее функцию распределения, плотность и т.п. Так, в силу закона больших
чисел выборочное среднее арифметическое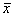 
является состоятельной оценкой математического
ожидания М(Х) (при любой функции распределения F(x) результатов наблюдений, для которой
математическое ожидание существует). С помощью центральной предельной теоремы
определяют асимптотические доверительные границы
(М(Х))Н =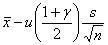 
, (М(Х))В = 
.
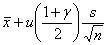где γ – доверительная
вероятность,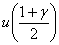 
- квантиль порядка 
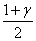стандартного нормального распределения N(0;1) с нулевым математическим
ожиданием и единичной дисперсией, 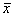- выборочное среднее арифметическое, s – выборочное среднее квадратическое
отклонение. Термин «асимптотические доверительные границы» означает, что
вероятности
P{(M(X))H < M(X)}, P{(M(X))B > M(X)},
P{(M(X))H < M(X) < (M(X))B}
стремятся к 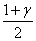, 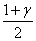и γ соответственно при n → ∞, но, вообще говоря,
не равны этим значениям при конечных n. Практически асимптотические
доверительные границы дают достаточную точность при n порядка 10.
