Точечное оценивание
Точечное оценивание - способ оценивания, заключающийся в
том, что значение оценки принимается как неизвестное значение параметра
распределения.
Пример 2. Пусть результаты наблюдений x1, x2,…, xn рассматривают в вероятностной модели
как случайную выборку из нормального распределения N(m,σ). Т.е. считают, что результаты
наблюдений моделируются как реализации n независимых одинаково распределенных
случайных величин, имеющих функцию нормального распределения N(m,σ) с некоторыми математическим
ожиданием m и
средним квадратическим отклонением σ, неизвестными статистику.
Требуется оценить параметры m и σ (или σ2) по
результатам наблюдений. Оценки обозначим m* и (σ2)* соответственно. Обычно
в качестве оценки m* математического ожидания m используют выборочное среднее
арифметическое 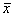 , а в
качестве оценки (σ2)* дисперсии σ2 используют выборочную дисперсию s2, т.е.
, а в
качестве оценки (σ2)* дисперсии σ2 используют выборочную дисперсию s2, т.е.
m* = 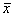 , (σ2)* = s2.
, (σ2)* = s2.
Для
оценивания математического ожидания m могут использоваться и другие
статистики, например, выборочная медиана 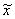 , полусумма минимального
и максимального членов вариационного ряда
, полусумма минимального
и максимального членов вариационного ряда
m** = [x(1)+x(n)]/2
и др. Для оценивания дисперсии σ2 также имеется ряд оценок, в частности, 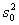 (см. выше) и оценка, основанная на размахе R, имеющая вид
(см. выше) и оценка, основанная на размахе R, имеющая вид
(σ2)** = [a(n)R]2,
где коэффициенты a(n) берут из специальных таблиц [8]. Эти коэффициенты
подобраны так, чтобы для выборок из нормального распределения
M[a(n)R] = σ.
Наличие
нескольких методов оценивания одних и тех же параметров приводит к
необходимости выбора между этими методами.

