Состоятельность и несмещенность критериев

Основной характеристикой статистического критерия является функция мощности. Для многих задач проверки статистических гипотез разработан не один статистический критерий, а целый ряд. Чтобы выбрать из них определенный критерий для использования в конкретной практической ситуации, проводят сравнение критериев по различным показателям качества [2, приложение 3], прежде всего с помощью их функций мощности. В качестве примера рассмотрим лишь два показателя качества критерия проверки статистической гипотезы – состоятельность и несмещенность.

Пусть объем выборки n растет, а U_n и Ψ_n – статистики критерия и критические области соответственно. Критерий называется состоятельным, если

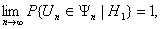
т.е. вероятность отвергнуть нулевую гипотезу стремится к 1, если верна альтернативная гипотеза.

Статистический критерий называется несмещенным, если для любого θ₀, удовлетворяющего Н₀, и любого θ₁ , удовлетворяющего Н₁, справедливо неравенство

P{U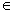Ψ | θ₀} < P{U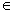Ψ | θ₁},

т.е. при справедливости Н₀ вероятность отвергнуть Н₀ меньше, чем при справедливости Н₁.

При наличии нескольких статистических критериев в одной и той же задаче проверки статистических гипотез следует использовать состоятельные и несмещенные критерии.