Подробнее о биномиальном распределении

Как уже говорилось, биномиальное распределение имеет место при независимых испытаниях, в каждом из которых с вероятностью р появляется событие А. Если общее число испытаний n задано, то число испытаний Y, в которых появилось событие А, имеет биномиальное распределение. Для биномиального распределения вероятность принятия случайной величиной Y значения y определяется формулой

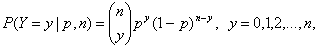   (19)

где

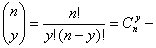
- число сочетаний из n элементов по y, известное из комбинаторики. Для всех y, кроме 0, 1, 2, …, n, имеем P(Y=y)=0. Биномиальное распределение при фиксированном объеме выборки n задается параметром p, т.е. биномиальные распределения образуют однопараметрическое семейство. Они применяются при анализе данных выборочных исследований [2], в частности, при изучении предпочтений потребителей, выборочном контроле качества продукции по планам одноступенчатого контроля, при испытаниях совокупностей индивидуумов в демографии, социологии, медицине, биологии и др.

Если Y₁ и Y₂ - независимые биномиальные случайные величины с одним и тем же параметром p₀, определенные по выборкам с объемами n₁ и n₂ соответственно, то Y₁ + Y₂ - биномиальная случайная величина, имеющая распределение (19) с р = p₀ и n = n₁ + n₂. Это замечание расширяет область применимости биномиального распределения, позволяя объединять результаты нескольких групп испытаний, когда есть основания полагать, что всем этим группам соответствует один и тот же параметр.

Характеристики биномиального распределения вычислены ранее:

M(Y) = np,  D(Y) = np(1-p).

В главе "События и вероятности" для биномиальной случайной величины доказан закон больших чисел:

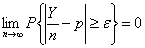
для любого 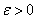. С помощью центральной предельной теоремы закон больших чисел можно уточнить, указав, насколько Y/n отличается от р. 

Теорема Муавра-Лапласа. Для любых чисел a и b, a<b, имеем

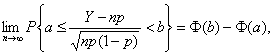
где Ф(х) – функция стандартного нормального распределения с математическим ожиданием 0 и дисперсией 1.

Для доказательства достаточно воспользоваться представлением Y в виде суммы независимых случайных величин, соответствующих исходам отдельных испытаний, формулами для M(Y) и D(Y) и центральной предельной теоремой.

Эта теорема для случая р = ½ доказана английским математиком А.Муавром (1667-1754) в 1730 г. В приведенной выше формулировке она была доказана в 1810 г. французским математиком Пьером Симоном Лапласом (1749 – 1827).