Логарифмически
нормальные распределения
Случайная величина Х имеет логарифмически
нормальное распределение, если случайная величина Y = lg X имеет нормальное распределение.
Тогда Z = ln X = 2,3026…Y также имеет нормальное распределение  N(a1,σ1), где ln X - натуральный логарифм Х.
Плотность логарифмически нормального распределения такова:
N(a1,σ1), где ln X - натуральный логарифм Х.
Плотность логарифмически нормального распределения такова:
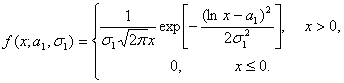
Из
центральной предельной теоремы следует, что произведение X = X1X2…Xn независимых положительных случайных
величин Xi, i = 1, 2,…, n, при больших n можно аппроксимировать логарифмически
нормальным распределением. В частности, мультипликативная модель формирования
заработной платы или дохода приводит к рекомендации приближать распределения
заработной платы и дохода логарифмически нормальными законами. Для России эта
рекомендация оказалась обоснованной - статистические данные подтверждают ее.
Имеются и другие
вероятностные модели, приводящие к логарифмически нормальному закону.
Классический пример такой модели дан А.Н.Колмогоровым [10], который из
физически обоснованной системы постулатов вывел заключение о том, что размеры
частиц при дроблении кусков руды, угля и т.п. на шаровых мельницах имеют логарифмически
нормальное распределение.

