|
А.И.
Орлов
Эконометрика
Учебник. М.: Издательство "Экзамен", 2002.
Приложение 1
Вероятностно-статистические
основы эконометрики
Эконометрика
опирается на твердый научный фундамент - теорию вероятностей и статистику. В
области теории вероятностей наша страна является признанным мировым лидером.
Практически все специалисты в этой области исходят в своей работе из аксиоматики
теории вероятностей, предложенной академиком А.Н. Колмогоровым в 1933 г. [1].
Однако
в отечественной и зарубежной литературе присутствуют различные интерпретации терминов
и разделов эконометрики, теории вероятностей, статистики. Одна из причин
состоит в том, что используют в своей работе эти научные области специалисты
разных профессий - экономисты, инженеры, математики… Поэтому мы приводим основную
терминологию и краткое описание математической статистики и ее новых разделов.
П1-1. Определения терминов
теории вероятностей и прикладной статистики
Определения
практически всех используемых в литературе понятий теории вероятностей и математической
статистики и основные сведения о соответствующих математических объектах
собраны в Энциклопедии [2]. Ниже приведены определения и обозначения (в стиле
[2]) лишь для основных понятий теории вероятностей и прикладной статистики,
используемых в настоящем учебном пособии. Как показали предыдущие публикации
(см., например, [3]), эта сводка позволяет осознанно изучать и применять
эконометрические методы для анализа конкретных экономических данных. Однако
она, очевидно, не заменяет систематических курсов теории вероятностей и
прикладной математической статистики, знакомство с которыми - необходимая
предпосылка для изучения эконометрики.
Споры
по поводу терминов весьма распространены. Весьма популярно желание добиться единства
терминологии. Однако практика терминологических дискуссий показывает, что
придти к единому мнению обычно не удается. Не помогают достижению единства и
административные меры, например, принятие государственных стандартов, "несоблюдение
которых карается по закону". Зачастую такие стандарты содержат в себе
много спорного, а то и ошибочного (подробнее об этом см. [3]).
Почти в каждой области
знания параллельно существуют различные терминологические системы. Большого
вреда это обычно не приносит. Так, операция умножения двух чисел a и b может быть обозначена четырьмя способами - крестиком (т.е. a х b),
точкой (a. b), отсутствием знака между сомножителями (ab) или звездочкой, как при программировании (a* b).
Случайные величины обозначают либо латинскими буквами, либо греческими. Для
математического ожидания используют либо символ М, либо символ Е,
и т.п.. Обычно можно без труда понять, о чем идет речь.
Однако при изучении
настоящего курса эконометрики необходимо пользоваться вполне определенной терминологической
системой. Она и приводится ниже. При этом мы отнюдь не отрицаем пригодности
других систем терминов и определений в тех или иных случаях.
№№ пп. |
Термины |
Определения |
Примечания |
| |
|
1. Теория вероятностей |
|
| |
|
1.1. Общие
понятия |
|
1.1.1. |
Пространство элементарных событий |
Множество, элементы которого,
называемые элементарными событиями, соответствуют возможным результатам
наблюдения, измерения, анализа, проверки, исходам опыта, эксперимента,
испытания. |
Пространство элементарных событий W = {w}
лежит в основе вероятностных моделей явлений (процессов). Вместо явного
описания пространства элементарных событий часто используют косвенное или
частичное
описание, например, с помощью
распределений случайных величин. |
1.1.2. |
Случайное событие |
Измеримое подмножество пространства элементарных
событий. |
Термин "измеримое" понимают в
смысле теории измеримых множеств. Случайные события образуют s-алгебру G. |
1.1.3. |
Вероятностная мера |
Сигма-аддитивная мера P, определенная
на всех случайных событиях и такая, что P(W)
= 1, где W - пространство элементарных событий |
Вероятностная мера P - функция,
ставящая в соответствие каждому случайному событию A его вероятность P(A).
Термин "мера" понимают в смысле математической теории меры.
Синонимы: вероятностное распределение, распределение вероятностей, распределение,
вероятность на пространстве элементарных событий. |
1.1.4. |
Вероятностное пространство |
Совокупность {W, G, P} пространства элементарных
событий W, класса случайных событий G и вероятностной меры
P. |
Вероятностное пространство (синоним:
поле вероятностей) - основной исходный объект теории вероятностей и
вероятностных моделей реальных явлений (процессов). |
1.1.5. |
Вероятность события A |
Значение P(A) вероятностной меры P на
случайном событии A. |
В силу закона больших чисел частота
реализации события A при неограниченном увеличении числа независимых
повторений одного и того же комплекса условий, описываемого вероятностным
пространством {W, G, P},
стремится к вероятности этого события P(A), т.е. для любого e > 0
limn®¥ P { | m/n - p | £ e } = 1,
где m/n - частота, p - вероятность события A, n - число повторений. Это
свойство нельзя принимать за определение вероятности события в математической
теории вероятностей. Оно указывает способ оценивания вероятности по опытным
данным. |
1.1.6. |
Независимость случайных событий |
Случайные события А и В являются независимыми,
если Р(АВ) = Р(А)Р(В), где АВ - пересечение
множеств А и В (произведение событий А и В). Случайные события А1, А2,..., Аn называются независимыми (в совокупности), если Р(А1А2...Аn)
= Р(А1)Р(А2)...Р(Аn) и аналогичные равенства
справедливы для всех поднаборов этих событий А(1), А(2),..., А(k), 2£k£n
-1. |
Общематематическое понятие пересечения
множеств АÇВ в теории вероятностей по традиции
эквивалентно понятию произведения событий АВ. |
1.1.7. |
Случайный элемент |
Измеримая функция, определенная на
вероятностном пространстве. |
Случайный элемент Х принимает значения
в измеримом пространстве (Z,J), где Z - пространство значений Х, а J - класс
измеримых подмножеств Z; при этом для любого QЄJ множество Х-1(Q) является случайным событием.
Если Z - множество действительных чисел
R1, то случайный элемент Х называют
случайной величиной. Если Z = Rk - конечномерное векторное пространство
размерности k=2,3,...., то случайный элемент Х называют случайным вектором. |
1.1.8. |
Распределение случайного элемента |
Функция множества, задающая вероятность
принадлежности случайного элемента измеримому подмножеству его области
значений. |
Для случайного элемента Х,
определенного на вероятностном пространстве {W,
G, P} со значениями в измеримом пространстве (Z,J), его распределение P1:J -® [0,1] задается формулой P1 (Q) = P (Х-1(Q)), QЄJ. |
1.1.9. |
Дискретный случайный элемент |
Случайный элемент, область значений которого
состоит из конечного или счетного множества точек. |
Распределение случайного элемента Х,
принимающего только значения х1, х2,..., полностью описывается числами рi = P(X=хi), i = 1,2,..., причем р1 + р2 +... = 1. |
1.1.10. |
Параметрическое семейство распределений |
Функция, определенная на
параметрическом пространстве (подмножестве конечномерного векторного
пространства), которая каждому значению параметра (числу или вектору, входящему
в параметрическое пространство) ставит в соответствие распределение случайного
элемента. |
Параметр может быть одномерным или
конечномерным. Вместо "зависимость от k-мерного параметра" часто
говорят "зависимость от k параметров". |
1.1.11. |
Независимость случайных элементов |
Определенные на одном и том же вероятностном
пространстве случайные элементы X1, X2,...,Xk со значениями в измеримых пространствах
(Z1,
J1), (Z2, J2),..., (Zk, Jk) соответственно называются
независимыми, если для любых Q1ЄJ1, Q2ЄJ2,..., QkЄJk имеем Р(X1ЄQ1, X2ЄQ2,..., XkЄQk) = Р(X1ЄQ1)P(X2ЄQ2)... P(XkЄQk). |
Для случайных величин и векторов,
имеющих плотности вероятности, независимость эквивалентна тому, что плотность
вероятности вектора (Х1, Х2,..., Хk) равна произведению плотностей
вероятностей случайных величин Хi, т.е.
f (x1, x2,..., xk) = f(x1)f(x2)...f(xk).
Результаты экспериментов, которые
проведены независимо друг от друга, как правило, моделируются с помощью
независимых случайных величин. |
1.1.12 |
Вероятностная модель явления (процесса) |
Математическая модель явления
(процесса), в которой использованы понятия теории вероятностей и
математической статистики. |
Установление (формулировка) исходной
вероятностной модели - необходимый первый этап для применения методов
прикладной статистики. |
| |
|
1.2.
Случайная величина |
|
1.2.1. |
Случайная величина |
Однозначная действительная измеримая
функция на вероятностном пространстве. |
Однозначная действительная функция X:W®R1 является случайной величиной, если для
любого хЄR1 множество {w:X(w) £ x} является случайным событием.
Случайная величина - это случайный элемент со значениями в R1. (Здесь R1 - множество действительных чисел.) |
1.2.2. |
Функция распределения |
Функция, определяющая для всех действительных
чисел х вероятность того, что случайная величина Х принимает значения,
меньшие х. |
Функция распределения F(x) = P(X <
x) = P{w:X(w)
< x}. Функция распределения непрерывна слева.
Примечание. Иногда функцию распределения определяют
как F(x) = P(X < x) = P{w:X(w) < x}. Тогда она непрерывна справа. |
1.2.3. |
Плотность вероятности |
Функция p(t) такая, что
 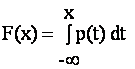
при всех х, где F(x) - функция
распределения рассматриваемой случайной величины. |
Сокращенная форма: плотность. |
1.2.4. |
Непрерывная случайная величина |
Случайная величина, функция
распределения которой при всех действительных x непрерывна. |
|
1.2.5. |
Квантиль порядка p |
Значение случайной величины, для
которого функция распределения принимает значение p или имеет место
"скачок" со значения меньше p до значения больше p. |
Число хр - квантиль порядка
р для случайной величины с функцией распределения F(x) тогда и только тогда,
когда
lim x®хр+0 F(x)³p, F(хр)£p.
Может случиться, что вышеуказанное
условие выполняется для всех значений х, принадлежащих некоторому интервалу.
Тогда каждое такое значение называется квантилью порядка р.
Примечание. Одни авторы употребляют
термин "квантиль" в мужском роде, другие - в женском. |
1.2.6. |
Медиана |
Квантиль порядка p = 1/2. |
|
1.2.7. |
Мода непрерывной случайной величины |
Значение случайной величины, соответствующее
локальному максимуму ее плотности вероятности. |
Мод у непрерывной случайной величины
может быть несколько (конечное число или бесконечно много).
Краткая форма термина: мода. |
1.2.8. |
Математическое ожидание |
Среднее взвешенное по вероятностям значение
случайной величины X(w), т.е.
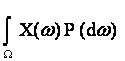 |
Математическое ожидание обозначают
М(Х), Е(Х), МХ, ЕХ и др. Рекомендуемое обозначение: М(Х). При этом
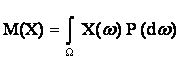 = = 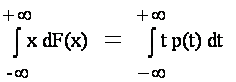
где F(x) - функция распределения, а
p(t) - плотность вероятности случайной величины Х = X(w).
Математическое ожидание существует не
для всех случайных величин Х. Для существования математического ожидания
необходимо и достаточно абсолютной сходимости соответствующего интеграла. |
1.2.9. |
Дисперсия (случайной величины X) |
Математическое ожидание квадрата
разности между случайной величиной и ее математическим ожиданием. |
Для случайной величины Х дисперсия D(X)
= s2=s2(X)=М(X-М(X))2. Дисперсия равна 0 тогда и только
тогда когда Р(Х=а)=1 для некоторого а. |
1.2.10. |
Среднее квадратическое отклонение |
Неотрицательный квадратный корень из дисперсии. |
|
1.2.11. |
Коэффициент вариации |
Отношение среднего квадратического отклонения
к математическому ожиданию. |
Применяется для положительных случайных
величин как показатель разброса. |
1.2.12. |
Момент порядка q (случайной величины X) |
Математическое ожидание случайной величины
Xq. |
|
1.2.13. |
Центральный момент порядка q (случайной
величины X) |
Математическое ожидание случайной величины
(X-М(X))q, где М(Х) - математическое ожидание Х. |
Дисперсия - центральный момент порядка
2. |
1.2.14. |
Характеристи-ческая функция (случайной
величины X) |
Функция от tЄR1 , при каждом t равная математическому
ожиданию случайной величины eitX, где i - мнимая единица, e -
основание натуральных логарифмов. |
М(eitX) = М(cos(tX) +
isin(tX)) = М(cos(tX)) + iМ(sin(tX)). |
| |
|
1.3.
Случайный вектор |
|
1.3.1. |
Случайный вектор |
Однозначная измеримая функция на вероятностном
пространстве со значениями в конечномерном евклидовом пространстве Rk. |
Случайный вектор Х - это случайный
элемент со значениями в Rk, т.е. X = X(w) = (X1(w),
X2(w),....,
Xk(w)),
где Xi(w), i = 1,2,...,k, - случайные величины,
заданные на одном и том же вероятностном пространстве. |
1.3.2. |
Функция распределения (случайного
вектора) |
Функция распределения F(x1, x2,...., xk) случайного вектора X(w)
= (X1(w), X2(w),....,
Xk(w))
удовлетворяет равенству
F(x1, x2,...., xk)
=
P (X1<x1, X2<x2,...,
Xk<xk) = P{ w:X1(w)< x1, X2(w)< x2,..., Xk(w)< xk). |
|
1.3.3. |
Плотность вероятности (случайного вектора) |
Функция p(x) такая, что
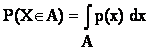
для случайного вектора X = X(w) и любого борелевского подмножества А
конечномерного евклидова пространства Rk. |
|
1.3.4. |
Математическое ожидание случайного вектора |
Вектор, компоненты которого - математические
ожидания компонент случайного вектора. |
Математическое ожидание случайного
вектора X = (X1,
X2,...., Xk) есть (М(X1), М(X2),...., М(Xk)), где М(Xi) - математическое ожидание случайной величины
Xi, являющейся i - ой компонентой случайного вектора X, i
= 1,2,...,k. |
1.3.5. |
Ковариация (для двумерного вектора) |
Ковариацией вектора (X,Y) называется
математическое ожидание случайной величины
(X - МX))(Y - М(Y)), где М(X) и М(Y) -
математические ожидания случайных величин X и Y. |
cov(X,Y)
= М (X
- М(X))(Y
- М(Y))
;
если X = Y, то cov(X,Y) = D(X) -
дисперсия X. |
1.3.6. |
Ковариационная матрица случайного вектора |
Квадратная матрица ||cij||
порядка k, в которой cij - ковариация двумерного вектора (Xi, Xj), где Xi и Xj - компоненты случайного вектора X = (X1, X2,...., Xk), i,j = 1,2,...,k. |
Ковариационная матрица симметрична, на
главной диагонали стоят дисперсии Xi - компонент X, i = 1,2,...,k. |
1.3.7. |
Коэффициент корреляции (для двумерного
вектора) |
Отношение ковариации вектора (X,Y) к произведению
средних квадратических отклонений s(X) и s(У)
случайных величин Х и У. |
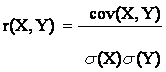
Если Y = aX+b, то |r(X,Y)| = 1. Верно и обратное: если |r(X,Y)| = 1, то Y = aX+b.. |
1.3.8. |
Корреляционная матрица случайного вектора |
Квадратная матрица ||rij||
порядка k, в которой rij - коэффициент корреляции двумерного вектора (Xi, Xj), где Xi и Xj - компоненты случайного вектора X = (X1, X2,...., Xk), i,j = 1,2,...,k. |
Корреляционная матрица симметрична, на
главной диагонали стоят единицы. |
| |
|
2. Прикладная статистика |
|
| |
|
2.1. Общие
понятия |
|
2.1.1. |
Признак |
Свойство (характеристика) объекта
наблюдения. |
Частными видами наблюдения являются
измерение, испытание, анализ, опыт, проверка и т.д. |
2.1.2. |
Результат наблюдения |
Значение признака объекта наблюдения. |
Результат наблюдения может быть числом,
вектором, элементом конечного множества или математическим объектом иной
природы. |
2.1.3. |
Выборка |
Совокупность значений одного и того же
признака у подвергнутых наблюдению объектов. |
Выборка - совокупность чисел или
векторов, или математических объектов иной природы, соответствующих изучаемым
реальным объектам наблюдения. |
2.1.4. |
Объем выборки |
Число результатов наблюдений,
включенных в выборку. |
Объем выборки обычно обозначают n. |
2.1.5. |
Вероятностная модель выборки |
Вероятностная модель получения
результатов наблюдений, включаемых в выборку. |
Примерами вероятностных моделей выборок
являются простая случайная выборка и случайная выборка из конечной совокупности. |
2.1.6. |
Простая случайная выборка |
Выборка, в которой результаты
наблюдений моделируются как совокупность независимых одинаково распределенных
случайных элементов. |
Если результаты наблюдений имеют
распределение F, то говорят, что "выборка извлечена из распределения
F". |
2.1.7. |
Случайная выборка из конечной совокупности |
Выборка объема n, в которую включены результаты
наблюдений над объектами, отбираемыми из конечной совокупности так, что любой
набор n объектов имеет одинаковую вероятность быть отобранным. |
Если N - число объектов конечной совокупности, то
для получения случайной выборки объема n из этой совокупности, n < N,
отбор объектов для проведения наблюдений должен проводиться так, чтобы любой
набор из n объектов имел одну и ту же вероятность быть отобранным, равную
n!(N-n)!/ N!, т.е. обратной величине к числу сочетаний из N элементов по n. |
2.1.8. |
Статистика |
Измеримая функция результатов
наблюдений, включенных в выборку, используемая для получения статистических
выводов. |
Статистики используются для описания
данных, оценивания, проверки гипотез. Статистика, как функция случайного
элемента, является случайным элементом. Статистика принимает значения в
некотором измеримом пространстве (Z,J), своем для каждой статистики. |
| |
|
2.2.
Описание данных |
|
2.2.1. |
Частота события |
Отношение числа наблюдений, в которых
осуществилось событие, к объему выборки. |
|
2.2.2. |
Эмпирическое распределение |
Распределение случайного элемента, в
котором каждому результату наблюдения, включенному в выборку, соответствует
одна и та же вероятность, равная обратной величине объема выборки. |
Если в выборку включены результаты
наблюдений x1,
x2,...., xn, то эмпирическое распределение - это распределение
случайной величины Х такой, что Р(Х= xi) = 1/n, i = 1,2,..., n. Если несколько результатов наблюдений
совпадают: x1 = x2 =.... = xk = a, то полагают Р(Х=а) = k/n. |
2.2.3. |
Эмпирическая функция распределения |
Функция эмпирического распределения. |
Определена, когда результаты наблюдений
- числа или вектора (функции распределения по пп.1.2.2 и 1.3.2
соответственно). |
2.2.4. |
Выборочное среднее арифметическое |
Сумма результатов наблюдений,
включенных в выборку, деленная на ее объем. |
Выборочное среднее арифметическое равно
математическому ожиданию случайной величины, имеющей эмпирическое распределение. |
2.2.5. |
Выборочная дисперсия |
Сумма квадратов отклонений результатов
наблюдений, включенных в выборку, от их выборочного среднего арифметического,
деленная на объем выборки. |
Выборочная дисперсия
s2 = 1/n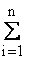 (хi - xср)2-, (хi - xср)2-,
где x1,
x2,...., xn - результаты наблюдений, включенные в
выборку; xср - выборочное среднее арифметическое,
xср = 1/n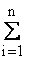 хi. хi.
Выборочная дисперсия равна дисперсии
случайной величины, имеющей эмпирическое распределение. |
2.2.6. |
Выборочное среднее квадратическое отклонение |
Неотрицательный квадратный корень из выборочной
дисперсии. |
|
2.2.7. |
Выборочный момент порядка q |
Момент порядка q случайной величины,
имеющей эмпирическое распределение. |
mq = 1/n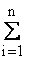 хiq, где хi по п.2.2.5. хiq, где хi по п.2.2.5. |
2.2.8. |
Выборочный центральный момент порядка q |
Центральный момент порядка q случайной
величины, имеющей эмпирическое распределение. |
mq = 1/n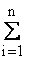 (хi - xср)q , где хi и xср по п.2.2.5. (хi - xср)q , где хi и xср по п.2.2.5. |
2.2.9. |
k-я порядковая статистика |
k-й элемент x(k) в вариационном ряду, полученном из
выборки объема n, элементы которой x1, x2,...., xn расположены в порядке неубывания: x(1)£x(2) £... £ x(k) £... £x(n). |
|
2.2.10. |
Размах выборки |
Разность между наибольшим и наименьшим
значениями результатов наблюдений в выборке. |
Если x(1) и x(n) - первая и n-ая порядковые статистики в
выборке объема n, то размах R = x(n) - x(1). |
2.2.11. |
Выборочная ковариация |
Ковариация двумерного случайного
вектора, имеющего эмпирическое распределение. |
Если (xi, yi),
i=1,2,....,n, - результаты наблюдений, включенные в выборку, то выборочная
ковариация равна 1/n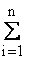 (хi - xср)(yi - yср),
где хi и xср по п.2.2.5, yср = 1/n (хi - xср)(yi - yср),
где хi и xср по п.2.2.5, yср = 1/n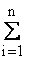 yi. yi. |
2.2.12. |
Выборочная ковариационная матрица |
Ковариационная матрица случайного
вектора, имеющего эмпирическое распределение. |
На главной диагонали выборочной
ковариационной матрицы стоят выборочные дисперсии по п.2.2.5, а вне главной
диагонали - выборочные ковариации по п.2.2.11. |
2.2.13. |
Выборочный коэффициент корреляции |
Коэффициент корреляции двумерного случайного
вектора, имеющего эмпирическое распределение. |
Выборочный коэффициент корреляции равен
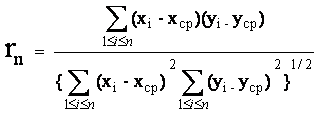
где хi и xср по
п.2.2.5, yi и yср по п.2.2.11. |
2.2.14. |
Выборочная корреляционная матрица |
Корреляционная матрица случайного вектора,
имеющего эмпирическое распределение. |
На главной диагонали выборочной
корреляционной матрицы стоят 1, а вне
главной диагонали - выборочные коэффициенты корреляции по п.2.2.13. |
2.2.15 |
Выборочный коэффициент вариации |
Отношение выборочного среднего квадратического
отклонения к выборочному среднему арифметическому. |
Выборочный коэффициент вариации
используют, когда результаты наблюдений положительны. |
| |
|
2.3.
Оценивание |
|
2.3.1. |
Оценивание |
Приближенное определение интересующей
специалиста составляющей вероятностной модели явления (процесса) по выборке. |
Составляющими вероятностных моделей
могут быть: значение параметра распределения; характеристика распределения
(математическое ожидание, коэффициент вариации и др.); функция распределения;
плотность вероятности; регрессионная зависимость, и т.д. |
2.3.2. |
Оценка |
Результат оценивания по конкретной выборке. |
Оценка является статистикой, а потому
случайным элементом, в частных случаях - случайной величиной или случайным
вектором. |
2.3.3. |
Точечное оценивание |
Вид оценивания, при котором для
оценивания используется одно определенное значение. |
|
2.3.4. |
Доверительное оценивание |
Вид оценивания, при котором для
оценивания используется множество. |
Рассматриваемое множество лежит в
пространстве возможных состояний оцениваемой составляющей вероятностной
модели явления (процесса). |
2.3.5. |
Доверительное множество |
Определяемое по выборке множество в пространстве
возможных состояний оцениваемой составляющей, используемое при доверительном
оценивании. |
Доверительное множество является
случайным множеством. |
2.3.6. |
Доверительная вероятность |
Вероятность того, что доверительное
множество содержит действительное значение оцениваемой составляющей. |
В конкретных задачах оценивания для
фиксированных доверительных вероятностей строят соответствующие доверительные
множества. |
2.3.7. |
Доверительный интервал |
Доверительное множество, являющееся интервалом. |
Интервалы могут быть как ограниченными,
так и неограниченными (лучами). |
2.3.8. |
Доверительные границы |
Концы (границы) доверительного интервала. |
|
2.3.9. |
Верхняя доверительная граница |
Граница доверительного интервала, являющегося
лучом, не ограниченным снизу. |
Для доверительного интервала (-¥; a)
верхней доверительной границей является число a. |
2.3.10. |
Нижняя доверительная граница |
Граница доверительного интервала, являющегося
лучом, не ограниченным сверху. |
Различие верхних, нижних и двусторонних
доверительных границ необходимо учитывать при проведении конкретных расчетов,
т.к. часто все виды границ определяются с помощью одних и тех же таблиц. |
2.3.11. |
Двусторонние доверительные границы |
Границы ограниченного (и сверху, и
снизу) доверительного интервала |
Для двусторонних границ (T1;T2) с вероятностью 1 справедливо
неравенство T1£T2. |
| |
|
2.4.
Проверка статистических гипотез |
|
2.4.1. |
Статистическая гипотеза |
Определенное предположение о свойствах
распределений случайных элементов, лежащих в основе наблюдаемых случайных явлений
(процессов). |
|
2.4.2. |
Нулевая гипотеза |
Статистическая гипотеза, подлежащая проверке
по статистическим данным (результатам наблюдений, вошедшим в выборку). |
Из возможных статистических гипотез в
качестве нулевой выбирают ту, прннятие справедливости которой наиболее важно
для дальнейших выводов. |
2.4.3. |
Альтернативная гипотеза |
Статистическая гипотеза, которая
считается справедливой, если нулевая гипотеза неверна. |
Сокращенная форма - альтернатива. |
2.4.4. |
Статистический критерий |
Правило, по которому на основе
результатов наблюдений принимается решение о принятии или отклонении нулевой
гипотезы. |
Принимаемое решение может однозначно
определяться по результатам наблюдений (нерандомизированный критерий) или в
некоторой степени зависеть от случая (рандомизированный критерий). |
2.4.5. |
Статистика критерия |
Статистика, на основе которой сформулировано
решающее правило. |
Как правило, нерандомизированный
статистический критерий основан на статистике критерия, принимающей числовые
значения. |
2.4.6. |
Критическая область статистического критерия |
Область в пространстве возможных
выборок со следующими свойствами: если наблюдаемая выборка принадлежит данной
области, то отвергают нулевую гипотезу (и принимают альтернативную), в
противном случае ее принимают (и отвергают альтернативную). |
Если статистический критерий основан на
статистике критерия, то критическая область статистического критерия
однозначно определяется по критической области статистики критерия.
Краткая форма: критическая область. |
2.4.7. |
Критическая область статистики критерия |
Множество чисел такое, что при
попадании в него статистики критерия нулевую гипотезу отвергают, в противном
случае принимают. |
Краткая форма: критическая область. |
2.4.8. |
Критические значения |
Границы (концы) одного или двух интервалов,
составляющих критическую область статистики критерия. |
Критическими значениями являются одно
или два из чисел t1,
t2 в случае, если
критическая область имеет вид {Tn<t1}, {Tn>t1} или {Tn<t1}È{Tn>t2}, где Tn - статистика критерия. |
2.4.9. |
Ошибка первого рода |
Ошибка, заключающаяся в том, что нулевую
гипотезу отвергают, в то время как в действительности эта гипотеза верна. |
|
2.4.10. |
Уровень значимости |
Вероятность ошибки первого рода или точная верхняя грань таких
вероятностей. |
Если нулевая гипотеза является сложной
(например, задается с помощью множества параметров Q0),
то вероятность ошибки первого рода может быть не числом (a), а
функцией (a(q0), q0ÎQ0). В качестве уровня значимости берут
точную верхнюю грань значений указанной функции:
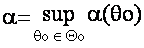 . .
|
2.4.11. |
Ошибка второго рода |
Ошибка, заключающаяся в том, что
нулевую гипотезу принимают, в то время как в действительности эта гипотеза
неверна (а верна альтернативная гипотеза). |
|
2.4.12. |
Мощность критерия |
Вероятность того, что нулевая гипотеза
будет отвергнута, если альтернативная гипотеза верна. |
Мощность критерия является однозначной
действительной функцией, определенной на составляющем альтернативу множестве
гипотез, заданном в конкретной задаче статистической проверки гипотез, в частности,
на параметрическом множестве, соответствующем альтернативным гипотезам. |
2.4.13. |
Функция мощности статистического критерия |
Функция, определяющая вероятность того,
что нулевая гипотеза будет отклонена. |
Функция мощности критерия задана на
множестве всех гипотез, используемых в конкретной задаче статистической
проверки гипотез. Сужением ее на нулевую гипотезу является функция, задающая
вероятность ошибки первого рода. Сужением ее на альтернативу является
мощность критерия. |
2.4.14. |
Оперативная характеристика статистического
критерия |
Функция, определяющая вероятность того,
что нулевая гипотеза будет принята. |
Оперативная характеристика - дополнение
до единицы функции мощности статистического критерия. |
2.4.15. |
Критерий согласия |
Критерий проверки гипотезы согласия,
т.е. того, что функция распределения результатов наблюдения, включенных в
простую случайную выборку, совпадает с заданной или входит в заданное
параметрическое семейство. |
|
2.4.16. |
Критерий однородности |
Критерий для проверки гипотезы о том,
что функции распределений результатов наблюдений из двух или нескольких
независимых простых случайных выборок совпадают (абсолютная однородность) или
отдельные их характеристики совпадают (однородность в смысле математических
ожиданий, коэффициентов вариации и т.д.). |
Рассматривают также критерии
независимости, симметрии, случайности, отбраковки и др. |
2.4.17. |
Номинальный (заданный) уровень значимости |
Число, используемое в статистических
таблицах, с помощью которого выбирают критическое значение статистики
критерия при проверке статистической гипотезы. |
Номинальный (заданный) уровень
значимости обычно берут равным 0,1; 0,05; 0,01. |
2.4.18. |
Реальный (истинный) уровень значимости |
Уровень значимости статистического критерия,
выбранного по номинальному уровню значимости. |
Из-за дискретности распределения
статистики критерия реальный уровень значимости может быть в несколько раз
меньше номинального. |
2.4.19. |
Достигаемый уровень значимости |
Случайная величина, равная вероятности
попадания статистики критерия в критическую область, заданную рассчитанным по
выборке значением статистики критерия. |
Для критической области вида {x:x>a}
достигаемый уровень значимости есть F(Xn), где Xn -
рассчитанное по выборке значение статистики критерия X, а F(a) = P(X>a) -
дополнение до 1 функции распределения статистики критерия X. Достигаемый
уровень значимости - это вероятность того, что статистика критерия Х в новом
независимом эксперименте примет значение большее, чем при расчете по
конкретной выборке, т.е. большее, чем Xn. |
2.4.20. |
Независимые выборки |
Выборки, объединение элементов которых
моделируется набором независимых (в совокупности) случайных элементов. |
См. п.1.1.11. |
П1-2. Математическая
статистика и ее новые разделы
Приведем
краткие описания (типа статей в энциклопедических изданиях) математической
статистики и ее наиболее важных для эконометрики сравнительно новых разделов,
разработанных в основном после 1970 г., а именно, статистики объектов
нечисловой природы и статистики интервальных данных.
Статистика
математическая - наука о математических методах анализа данных, полученных при проведении
массовых наблюдений (измерений, опытов). В зависимости от математической
природы конкретных результатов наблюдений статистика математическая делится на статистику чисел, многомерный статистический анализ, анализ функций
(процессов) и временных рядов, статистику объектов нечисловой природы. Существенная
часть статистики математической основана на вероятностных
моделях.
Выделяют общие задачи
описания данных, оценивания и проверки гипотез. Рассматривают и более частные
задачи, связанные с проведением выборочных обследований, восстановлением зависимостей,
построением и использованием классификаций (типологий) и др.
Для описания данных
строят таблицы, диаграммы, иные наглядные представления, например, корреляционные
поля. Вероятностные модели обычно не применяются. Некоторые методы описания
данных опираются на продвинутую теорию и возможности современных компьютеров. К
ним относятся, в частности, кластер-анализ, нацеленный на выделение групп
объектов, похожих друг на друга, и многомерное шкалирование, позволяющее
наглядно представить объекты на плоскости, в наименьшей степени исказив
расстояния между ними.
Методы оценивания и
проверки гипотез опираются на вероятностные модели порождения данных. Эти
модели делятся на параметрические и непараметрические. В параметрических
моделях предполагается, что изучаемые объекты описываются функциями распределения,
зависящими от небольшого числа (1-4) числовых параметров. В непараметрических
моделях функции распределения предполагаются произвольными непрерывными. В статистике математической оценивают параметры и характеристики распределения (математическое
ожидание, медиану, дисперсию, квантили и др.), плотности и функции распределения,
зависимости между переменными (на основе линейных и непараметрических
коэффициентов корреляции, а также параметрических или непараметрических оценок
функций, выражающих зависимости) и др. Используют точечные и интервальные
(дающие границы для истинных значений) оценки.
В статистике математической есть общая теория проверки гипотез и большое число методов, посвященных
проверке конкретных гипотез. Рассматривают гипотезы о значениях параметров и
характеристик, о проверке однородности (т.е. о совпадении характеристик или
функций распределения в двух выборках), о согласии эмпирической функции
распределения с заданной функцией распределения или с параметрическим семейством
таких функций, о симметрии распределения и др.
Большое значение для
эконометрики имеет раздел статистики математической, связанный с
проведением выборочных обследований, со свойствами различных схем организации
выборок и построением адекватных методов оценивания и проверки гипотез.
Задачи восстановления
зависимостей активно изучаются более 200 лет, с момента разработки К. Гауссом в
1794 г. метода наименьших квадратов. В настоящее время наиболее актуальны
методы поиска информативного подмножества переменных и непараметрические
методы.
Различные методы
построения (кластер-анализ), анализа и использования (дискриминантный анализ)
классификаций (типологий) именуют также методами распознавания образов (с
учителем и без), автоматической классификации и др.
Математические методы в
статистике основаны либо на использовании сумм (на основе Центральной
Предельной Теоремы теории вероятностей) или показателей различия (расстояний,
метрик), как в статистике объектов нечисловой природы. Строго обоснованы обычно
лишь асимптотические результаты. В настоящее время компьютеры играют большую
роль в статистике математической. Они используются как для расчетов,
так и для имитационного моделирования (в частности, в методах размножения
выборок и при изучении пригодности асимптотических результатов).
Классическая статистика математическая лучше всего представлена в [2,4]. По историческим причинам
основные российские работы публикуются в [3]. Обзор современного состояния статистики математической дан в [6].
Статистика объектов
нечисловой природы -
раздел математической статистики, в котором статистическими данными являются
объекты нечисловой природы, т.е. элементы множеств, не являющихся линейными
пространствами. Объекты нечисловой природы нельзя складывать и умножать на
число. Примерами являются результаты измерений в шкалах наименований, порядка,
интервалов; ранжировки, разбиения, толерантности и другие бинарные отношения;
результаты парных и множественных сравнений; люсианы, т.е. конечные последовательности
из 0 и1; множества; нечеткие множества. Необходимость применения объектов
нечисловой природы возникает во многих областях научной и практической
деятельности, в том числе и в социологии. Примерами являются ответы на "закрытые"
вопросы в эконометрических, маркетинговых, социологических анкетах, в которых
респондент должен выбрать одну или несколько из фиксированного числа подсказок,
мили измерение мнений о привлекательности (товаров, услуг, профессий, политиков
и др.), проводимое по порядковой шкале. Наряду со специальными теориями для каждого
отдельного вида объектов нечисловой природы в статистике объектов нечисловой природы имеется и теория
обработки данных, лежащих в пространстве общей природы, результаты которой
применимы во всех специальных теориях.
В статистике объектов
нечисловой природы классические задачи математической статистики - описание
данных, оценивание, проверку гипотез - рассматривают для данных неклассического
типа, что приводит к своеобразию постановок задач и методов их решения. Например,
из-за отсутствия линейной структуры в пространстве, в котором лежат статистические
данные, в статистике объектов нечисловой природы математическое ожидание
определяют не через сумму или интеграл, как в классическом случае, а как
решение задачи минимизации некоторой функции. Эта функция представляет собой
математическое ожидание (в классическом смысле) показателя различия между
значением случайного объекта нечисловой природы и фиксированным элементом
пространства. Эмпирическое среднее определяют как результат минимизации суммы
расстояний от нечисловых результатов наблюдений до фиксированного элемента
пространства. Справедлив закон больших чисел: эмпирическое среднее сходится при
увеличении объема выборки к математическому ожиданию, если результаты наблюдений
являются независимыми одинаково распределенными случайными объектами нечисловой
природы и выполнены некоторые математические "условия регулярности".
Аналогичным образом
определяют условное математическое ожидание и регрессионную зависимость. Из доказанной
в статистике объектов нечисловой природы сходимости решений
экстремальных статистических задач к решениям соответствующих предельных задач
вытекает состоятельность оценок в параметрических задачах оценивания параметров
и аппроксимации, а также ряд результатов в многомерном статистическом анализе.
Большую роль в статистике объектов нечисловой природы играют
непараметрические методы, в частности, методы непараметрической оценки
плотности и регрессионной зависимости в пространствах общей природы, в том
числе и в дискретных пространствах.
Для решения многих задач
статистики объектов нечисловой природы - нахождения эмпирического
среднего, оценки регрессионной зависимости, классификации наблюдений и др. -
используют показатели различия (меры близости, расстояния, метрики) между элементами
рассматриваемых пространств, вводимые аксиоматически. Так, в монографии [7]
аксиоматически введено расстояние между множествами. Принятое в теории
измерений как части статистики объектов нечисловой природы условие
адекватности (инвариантности) алгоритмов анализа данных позволяет указать вид
средних величин, расстояний, показателей связи и т.д., соответствующих
измерениям в тех или иных шкалах. Методы построения, анализа и использования
классификаций и многомерного шкалирования дают возможность сжать информацию и
дать ей наглядное представление. К статистике объектов нечисловой природы относятся
методы ранговой корреляции, статистического анализа бинарных отношений
(ранжировок, разбиений, толерантностей), параметрические и непараметрические
методы обработки результатов парных и множественных сравнений. Теория люсианов
(последовательностей независимых испытаний Бернулли) развита в асимптотике растущей
размерности.
Статистика объектов
нечисловой природы как
самостоятельный раздел прикладной математической статистики выделена в
монографии [7]. Обзору ее основных направлений посвящен, например, сборник [8].
Ей посвящен раздел в энциклопедии [2].
Статистика интервальных
данных (СИД)
- раздел статистики объектов нечисловой природы, в котором элементами
выборки являются интервалы в R, в частности, порожденные наложением ошибок
измерения на значения случайных величин. СИД входит в теорию устойчивости
(робастности) статистических процедур (см. [7]) и примыкает к интервальной
математике (см. [9]). В СИД изучены проблемы регрессионного анализа, планирования
эксперимента, сравнения альтернатив и принятия решений в условиях интервальной
неопределенности и др. (см.[10-13]).
Развиты асимптотические
методы статистического анализа интервальных данных при больших объемах выборок
и малых погрешностях измерений. В отличие от классической математической
статистики, сначала устремляется к бесконечности объем выборки и только потом -
уменьшаются до нуля погрешности. Разработана общая схема исследования (см.
[14]), включающая расчет двух основных характеристик СИД - н о т н ы
(максимально возможного отклонения статистики, вызванного интервальностью
исходных данных) и р а ц и о н а л ь н
о г о о б ъ е м а в ы б о р к и (превышение которого не дает
существенного повышения точности оценивания и статистических выводов, связанных
с проверкой гипотез). Она применена к оцениванию математического ожидания и
дисперсии, медианы и коэффициента вариации, параметров гамма-распределения в
ГОСТ 11.011-83 [15] и характеристик аддитивных статистик, для проверки гипотез
о параметрах нормального распределения, в т.ч. с помощью критерия Стьюдента, а
также гипотезы однородности двух выборок по критерию Смирнова, и т.д..
Разработаны подходы СИД в основных постановках регрессионного, дискриминантного
и кластерного анализов (см. [16]).
Многие
утверждения СИД отличаются от аналогов из классической математической
статистики. В частности, не существует состоятельных оценок: средний квадрат
ошибки оценки, как правило, асимптотически равен сумме дисперсии этой оценки,
рассчитанной согласно классической теории, и квадрата нотны. Метод моментов иногда оказывается
точнее метода максимального правдоподобия (см. [15, 17]). Нецелесообразно с целью
повышения точности выводов увеличивать
объем выборки сверх некоторого предела. В СИД классические доверительные
интервалы должны быть расширены вправо и влево на величину нотны, и длина их не
стремится к 0 при росте объема выборки.
Многим задачам
классической математической статистики могут быть поставлены в соответствие
задачи СИД, в которых элементы выборок - действительные числа заменены на
интервалы. В статистическое программное обеспечение включают алгоритмы СИД,
"параллельные" их аналогам из
классической математической статистики. Это позволяет учесть наличие погрешностей
у результатов наблюдений.
Цитированная литература
1. Колмогоров А.Н. Основные понятия теории
вероятностей. 2-е изд. - М.: Наука, 1974. - 120 с.
2. Вероятность и математическая статистика.
Энциклопедия / Гл. ред. Ю. В. Прохоров. – М.: Изд-во «Большая Российская Энциклопедия»,
1999. – 910 с.
3. Орлов А.И. Термины и
определения в области вероятностно-статистических методов. – Журнал «Заводская
лаборатория». 1999. Т.65. No.7. С.46-54.
4. Большев Л.Н., Смирнов Н.В. Таблицы
математической статистики. - М.: Наука, 1983.
5. Секция "Математические методы
исследования" журнала "Заводская лаборатория. Диагностика
материалов".
6. Орлов А.И. Современная прикладная статистика.
- Журнал "Заводская лаборатория". 1998. Т.64. No.3.
С. 52-60.
7. Орлов А.И. Устойчивость в
социально-экономических моделях. - М.: Наука, 1979. - 296 с.
8. Анализ нечисловой информации в
социологических исследованиях. - М.: Наука, 1985. - 220 с.
9. Шокин Ю.И. Интервальный анализ. -
Новосибирск: Наука, 1981. - 112 с.
10. Вощинин А.П. Метод
оптимизации объектов по интервальным моделям целевой функции. - М.: МЭИ, 1987.
- 109 с.
11. Вощинин А.П.,
Сотиров Г.Р. Оптимизация в условиях неопределенности. - М.: МЭИ - София:
Техника, 1989. - 224 с.
12. Кузнецов В.П. Интервальные статистические
модели. - М.: Радио и связь, 1991. - 352 с.
13. Сборник трудов Международной конференции по
интервальным и стохастическим методам в науке и технике (ИНТЕРВАЛ-92). Тт. 1,2.
- М.: МЭИ, 1992. - 216 с., 152 с.
14. Орлов А.И. О развитии реалистической
статистики. - В сб.: Статистические методы оценивания и проверки гипотез. Межвузовский
сборник научных трудов. Пермь: Изд-во Пермского государственного университета,
1990, с..89-99.
15. ГОСТ 11.011-83. Прикладная статистика.
Правила определения оценок и доверительных границ для параметров
гамма-распределения. - М.: Изд-во стандартов, 1984. - 53 с.
16. Орлов А.И. Интервальный статистический
анализ. - В сб.: Статистические методы оценивания и проверки гипотез. Межвузовский
сборник научных трудов. Пермь: Пермский государственный университет, 1993,
с.149-158.
17. Орлов А.И. Интервальная статистика: метод
максимального правдоподобия и метод моментов. - В сб.: Статистические методы
оценивания и проверки гипотез. Межвузовский сборник научных трудов. - Пермь:
Изд-во Пермского государственного университета, 1995, с.114-124.
Материал предоставлен сайтом AUP.Ru (Электронная библиотека экономической и деловой литературы)
|

